平衡二叉树

平衡二叉树，又称AVL树，指的是左子树上的所有节点的值都比根节点的值小， 而右子树上的所有节点的值都比根节点的值大，且左子树与右子树的高度差最大为1。 因此，平衡二叉树满足所有二叉排序（搜索）树的性质。 至于AVL，则是取自两个发明平衡二叉树的科学家的名字：G. M. Adelson-Velsky和E. M. Landis。

有了二叉排序树就可以使插入、搜索效率大大提高了，为什么还要引入平衡二叉树？

二叉搜索树的结构与值的插入顺序有关，同一组数，若其元素的插入顺序不同，二叉搜索树的结构是千差万别的。举个例子，给出一组数[1,3,5,8,9,13]。

若按照[5,1,3,9,13,8]这样的顺序插入，其流程是这样的：

若按照[1,3,5,8,9,13]这样的顺序插入，其流程是这样的：

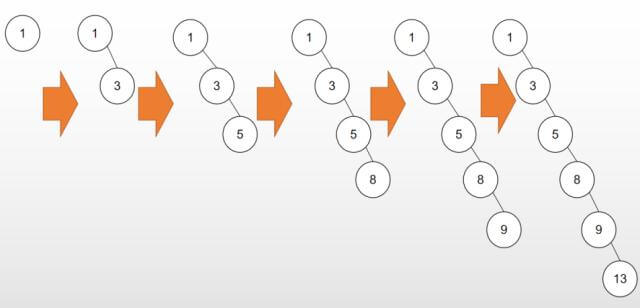
依据此序列构造的二叉搜索树为右斜树，同时二叉树退化成单链表，搜索效率降低为O(n)。

为了避免二叉搜索树变成“链表”，我们引入了平衡二叉树，即让树的结构看起来尽量“均匀”，左右子树的节点数尽量一样多。

生成平衡二叉树

那给定插入序列，如何生成一棵平衡二叉树呢？

先按照生成二叉搜索树的方法构造二叉树，直至二叉树变得不平衡， 即出现这样的节点：左子树与右子树的高度差大于1。 至于如何调整，要看插入的导致二叉树不平衡的节点的位置。 主要有四种调整方式：LL（左旋）、RR（右旋）、LR（先左旋再右旋）、RL（先右旋再左旋）。

平衡因子

某节点的左子树与右子树的高度(深度)差即为该节点的平衡因子（BF,Balance Factor）， 平衡二叉树中不存在平衡因子大于1的节点。 在一棵平衡二叉树中，节点的平衡因子只能取-1、1或者0。

对于给定结点数为n的AVL树，最大高度为O(log2n).

定义节点

    private class Node<E>{
        E data;
        Node<E> lchild;
        Node<E> rchild;

        Node(E element){
            this.data = element;
        }
    }

左旋

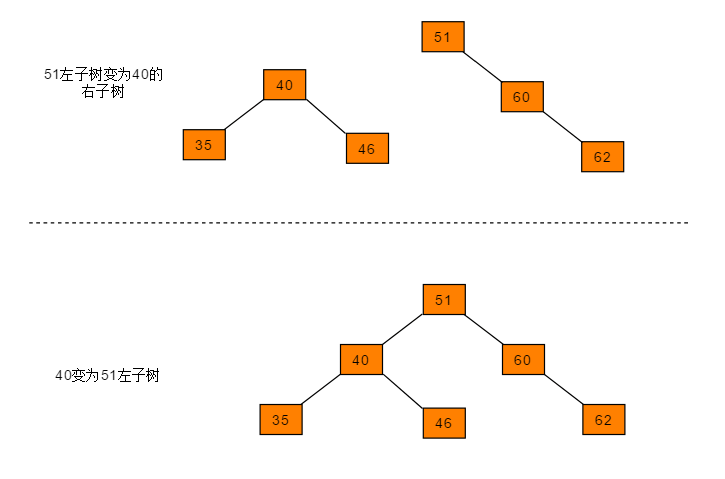
如下图所示的平衡二叉树

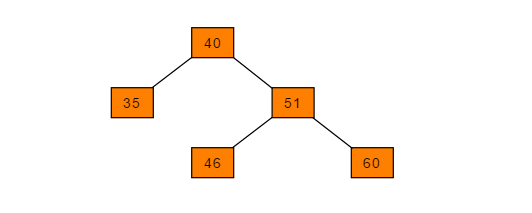
如在此平衡二叉树插入节点62，树结构变为：

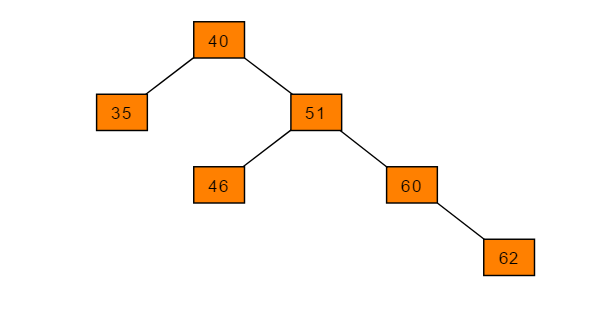
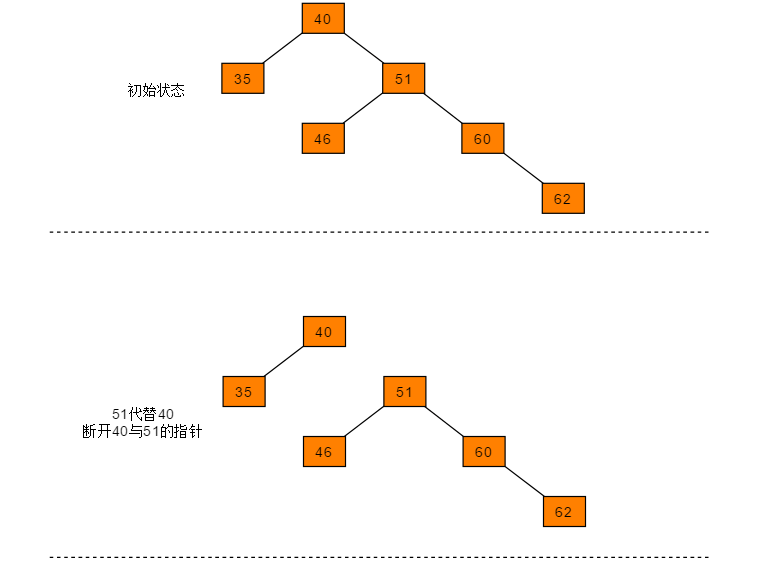
可以得出40节点的左子树高度为1，右子树高度为3，此时平衡因子为-2，树失去平衡。 为保证树的平衡，此时需要对节点40做出旋转，因为右子树高度高于左子树，对节点进行左旋操作，流程如下：

1. 节点的右孩子替代此节点位置
2. 右孩子的左子树变为该节点的右子树
3. 节点本身变为右孩子的左子树

图解过程：

然而更多时候根节点并不是只有一个子树，下图为复杂的LL（左旋，插入13导致值为4的节点不平衡）：

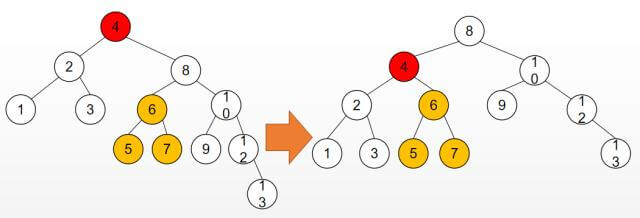
红色节点为插入后不平衡的节点， 黄色部分为需要改变父节点的分支，左旋后， 原红色节点的右孩子节点变成了根节点， 红色节点变成了它的左孩子， 而它原本的左孩子（黄色部分）不能丢， 而此时红色节点的右孩子是空的， 于是就把黄色部分放到了红色节点的右孩子的位置上。 调整后该二叉树还是一棵二叉排序（搜索）树， 因为黄色部分的值大于原来的根节点的值， 而小于后来的根节点的值，调整后， 黄色部分还是位于原来的根节点（红色节点）和后来的根节点之间。

    /**
     * 左旋
     *
     * @param e
     * @return 返回的是左旋后的根节点，左旋后的根节点是原来根节点的右孩子，左旋后的根节点的左孩子需要嫁接到原来根节点的右孩子上，原来的根节点嫁接到左旋后根节点的左孩子上。temp对应上图中值为8的节点，root对应上图中值为4的节点。
     */
    private Node<E> leftRotate(Node<E> e){
        Node<E> temp = e.rchild;
        e.rchild = temp.lchild;
        temp.lchild = e;
        return temp;
    }

右旋

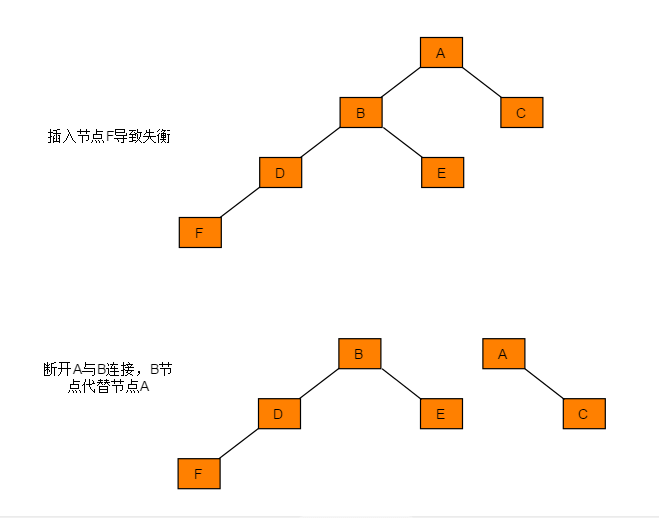
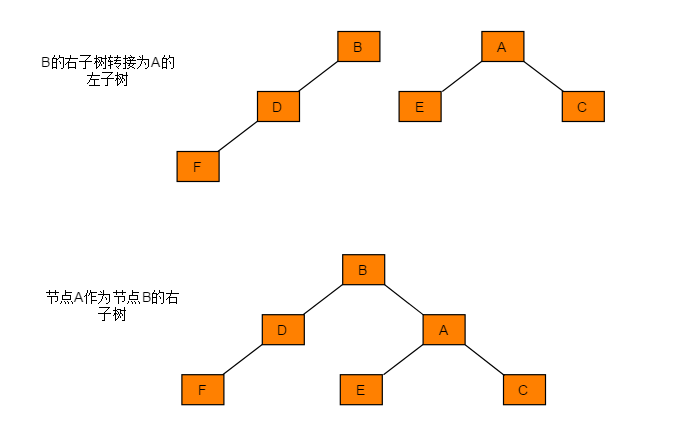
右旋操作与左旋类似，操作流程为：

1. 节点的左孩子代表此节点
2. 节点的左孩子的右子树变为节点的左子树
3. 将此节点作为左孩子节点的右子树。

图解过程：

然而更多时候根节点并不是只有一个子树，下图为复杂的RR（右旋，插入1导致值为9的节点不平衡）：

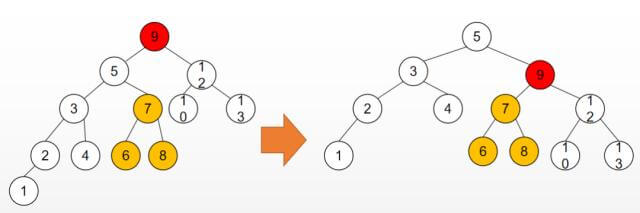
红色节点为插入后不平衡的节点，黄色部分为需要改变父节点的分支，右旋后，原红色节点的左孩子节点变成了根节点，红色节点变成了它的右孩子， 而它原本的右孩子（黄色部分）不能丢，而此时红色节点的左孩子是空的，于是就把黄色部分放到了红色节点的左孩子的位置上。调整后该二叉树还是一棵二叉排序（搜索）树，因为黄色部分的值小于原来的根节点的值，而大于后来的根节点的值，调整后，黄色部分还是位于后来的根节点和原来的根节点（红色节点）之间。

右旋代码如下：

    /**
     * 右旋 返回的是右旋后的根节点，右旋后的根节点是原来根节点的左孩子，右旋后的根节点的右孩子需要嫁接到原来根节点的左孩子上，原来的根节点嫁接到右旋后根节点的右孩子上。temp对应上图中值为5的节点，root对应上图中值为9的节点。
     * @param e
     * @return
     */
    private Node<E> rightRotate(Node<E> e){
        Node<E> temp = e.lchild;
        e.lchild = temp.rchild;
        temp.rchild = e;
        return temp;
    }

先左旋再右旋

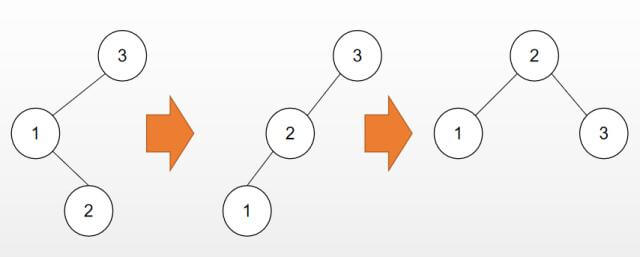
所谓LR（先左旋再右旋）就是先将左子树左旋，再整体右旋， 下图为最简洁的LR旋转（插入2导致值为3的节点不平衡）：

然而更多时候根节点并不是只有一个子树， 下图为复杂的LR旋转（插入8导致值为9的节点不平衡）：

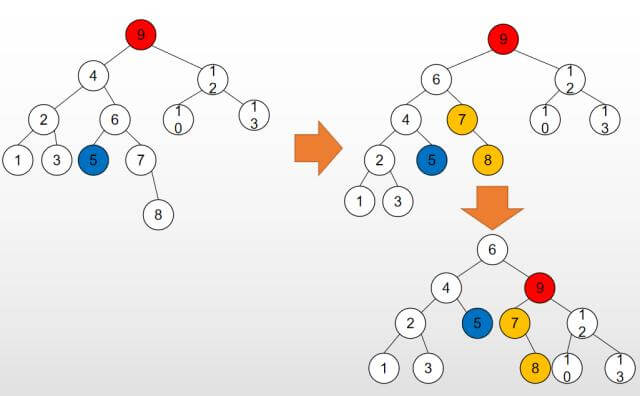
先将红色节点的左子树左旋，红色节点的左子树的根原本是值为4的节点， 左旋后变为值为6的节点，原来的根节点变成了左旋后根节点的左孩子， 左旋后根节点原本的左孩子（蓝色节点）变成了原来的根节点的右孩子； 再整体右旋，原来的根节点（红色节点）变成了右旋后的根节点的右孩子， 右旋后的根节点原本的右孩子（黄色节点）变成了原来的根节点（红色节点）的左孩子。旋转完成后， 仍然是一棵二叉排序（搜索）树。

LR旋转代码如下

/**
     * 先左旋再右旋
     * @param element
     * @return 返回的是LR旋转后的根节点，先对根节点的左子树左旋，再整体右旋。root对应上图中值为9的节点。
     */
    private Node<E> leftRightRotate(Node<E> element){

        //先对element的左子树左旋
        element.lchild = this.leftRotate(element.lchild);
        //再对element右旋
        return rightRotate(element);
    }

先右旋再左旋

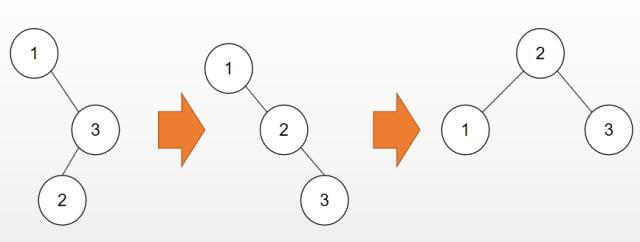
所谓RL（先右旋再左旋）就是先将右子树右旋，再整体左旋，下图为最简洁的RL旋转（插入2导致值为1的节点不平衡）：

然而更多时候根节点并不是只有一个子树，下图为复杂的RL旋转（插入8导致值为4的节点不平衡）：

先将红色节点的右子树右旋，红色节点的右子树的根原本是值为9的节点，右旋后变为值为6的节点， 原来的根节点变成了右旋后根节点的右孩子， 右旋后根节点原本的右孩子（蓝色节点）变成了原来的根节点的左孩子； 再整体左旋，原来的根节点（红色节点）变成了左旋后的根节点的左孩子， 左旋后的根节点原本的左孩子（黄色节点）变成了原来的根节点（红色节点）的右孩子。 旋转完成后，仍然是一棵二叉排序（搜索）树。

RL旋转代码如下：

/**
     *
     * @param element
     * @return 返回的是RL旋转后的根节点，先对根节点的右子树右旋，再整体左旋。root对应上图中值为4的节点。
     */
    private Node<E> rightLeftRotate(Node<E> element){

        //先对element的左子树左旋
        element.rchild = this.rightRotate(element.rchild);
        //再对element右旋
        return leftRotate(element);
    }

插入

假设一颗 AVL 树的某个节点为A，有四种操作会使 A 的左右子树高度差大于 1， 从而破坏了原有 AVL 树的平衡性。平衡二叉树插入节点的情况分为以下四种：

• A的左孩子的左子树插入节点(LL)

出现不平衡时到底是执行LL、RR、LR、RL中的哪一种旋转，取决于插入的位置。 可以根据值的大小关系来判断插入的位置。插入到不平衡节点的右子树的右子树上， 自然是要执行LL旋转；插入到不平衡节点的左子树的左子树上，自然是要执行RR旋转； 插入到不平衡节点的左子树的右子树上，自然是要执行LR旋转；插入到不平衡节点的右子树的左子树上， 自然是要执行RL旋转。

若向平衡二叉树中插入一个新结点后破坏了平衡二叉树的平衡性。 首先要找出插入新结点后失去平衡的最小子树根结点的指针。 然后再调整这个子树中有关结点之间的 链接关系，使之成为新的平衡子树。 当失去平衡的最小子树被调整为平衡子树后，原有其他所有不平衡子树无需调整， 整个二叉排序树就又成为一棵平衡二叉树。

失去平衡的最小子树是指以离插入结点最近，且平衡因子绝对值大于1的结点作为根的子树。 假设用A表示失去平衡的最小子树的根结点，则调整该子树的操作可归纳为下列四种情况。

• LL型平衡旋转法

由于在A的左孩子B的左子树上插入结点F，使A的平衡因子由1增至2而失去平衡。故需进行一次顺时针旋转操作。 即将A的左孩子B向右上旋转代替A作为根结点，A向右下旋转成为B的右子树的根结点。而原来B的右子树则变成A的左子树。

• RR型平衡旋转法

由于在A的右孩子C 的右子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。故需进行一次逆时针旋转操作。即将A的右孩子C向左上旋转代替A作为根结点，A向左下旋转成为C的左子树的根结点。而原来C的左子树则变成A的右子树。

• LR型平衡旋转法

由于在A的左孩子B的右子数上插入结点F，使A的平衡因子由1增至2而失去平衡。故需进行两次旋转操作（先逆时针，后顺时针）。即先将A结点的左孩子B的右子树的根结点D向左上旋转提升到B结点的位置，然后再把该D结点向右上旋转提升到A结点的位置。即先使之成为LL型，再按LL型处理。

• RL型平衡旋转法

由于在A的右孩子C的左子树上插入结点F，使A的平衡因子由-1减至-2而失去平衡。故需进行两次旋转操作（先顺时针，后逆时针），即先将A结点的右孩子C的左子树的根结点D向右上旋转提升到C结点的位置，然后再把该D结点向左上旋转提升到A结点的位置。即先使之成为RR型，再按RR型处理。

   public void add(E element) {
        Node<E> newNode = new Node<>(element);
        root = this.insert(root, newNode);
    }

    private Node<E> insert(Node<E> origin, Node<E> newNode) {
        if (origin == null) {

            origin = newNode;

        } else if (origin.data.compareTo(newNode.data) < 0) {
            //小
            origin.rchild = insert(origin.rchild, newNode);

        } else {
            //大等于
            origin.lchild = insert(origin.lchild, newNode);
        }

        boolean balance = isBalance(origin);
        if (!balance){
            origin = adjustment(origin, newNode);
        }

        return origin;
    }

    private Node<E> adjustment(Node<E> origin, Node<E> newNode) {

        if (origin.lchild != null && origin.lchild.data.compareTo(newNode.data) > 0 ){
            //新节点小于不平衡节点的左节点则是插入了左子树的左子树
            //RR型
            return rightRotate(origin);
        }

        if (origin.rchild.data.compareTo(newNode.data) < 0){
           //新节点大于不平衡节点的右节点则是插入了右子树的右子树
            //LL型
            return leftRotate(origin);
        }

        if (origin.lchild.data.compareTo(newNode.data) < 0 ){
            //新节点大于不平衡节点的左节点则是插入了左子树的右子树
            //LR型
            return leftRightRotate(origin);
        }

        if (origin.rchild.data.compareTo(newNode.data) > 0){
            //新节点小于不平衡节点的右节点则是插入了右子树的左子树
            //RL型
            return rightRotate(origin);
        }

        return origin;
    }

    private boolean isBalance(Node<E> origin) {
        return isBalancedTreeHelper(origin).balanced;
    }

    private TreeInfo isBalancedTreeHelper(Node<E> origin) {

        if (origin == null){
            return  new TreeInfo(-1, true);
        }

        // Check subtrees to see if they are balanced.
        TreeInfo left = isBalancedTreeHelper(origin.lchild);
        if (!left.balanced) {
            return new TreeInfo(-1, false);
        }
        TreeInfo right = isBalancedTreeHelper(origin.rchild);
        if (!right.balanced) {
            return new TreeInfo(-1, false);
        }
        // Use the height obtained from the recursive calls to
        // determine if the current node is also balanced.
        if (Math.abs(left.height - right.height) < 2) {
            return new TreeInfo(Math.max(left.height, right.height) + 1, true);
        }
        return new TreeInfo(-1, false);
    }

删除

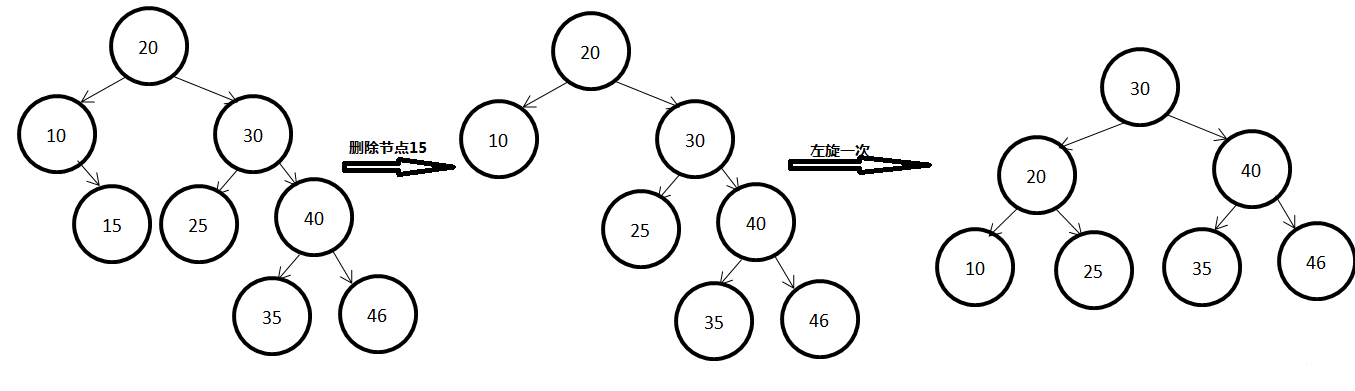
比如要下从下图中删除节点20

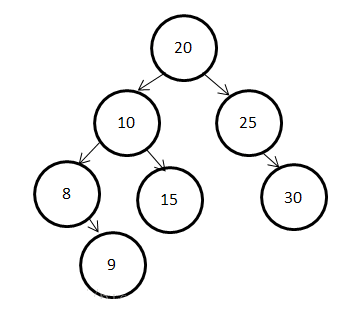
首先找到替换20被删除的节点15，并将二者内容替换，如下图所示：

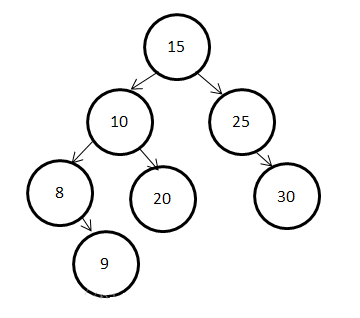
然后删除节点20得到下图：

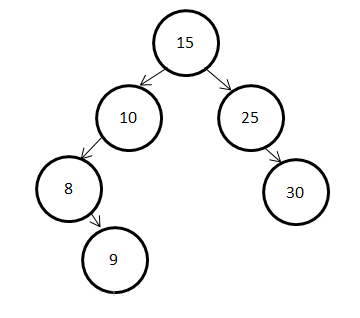
在删除节点20后，节点10违反了平衡二叉树的性质，对以10为根节点的子树进行调整（类似于插入时，需要先做一次左旋再做一次右旋）可得下图：

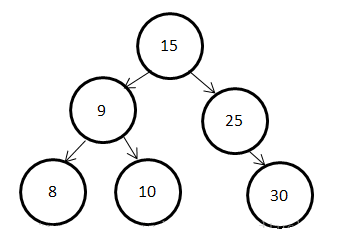
另一种情形如下图所示：

另一种情形如下图所示：

另一种情形如下图所示：

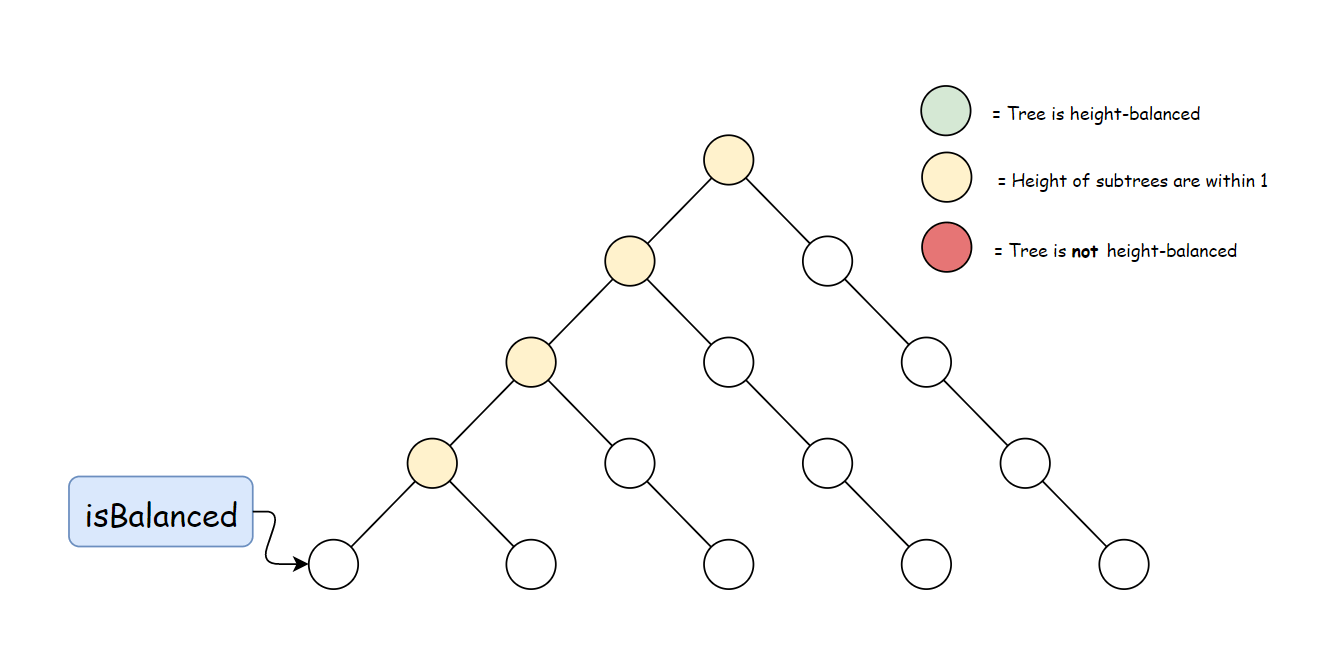
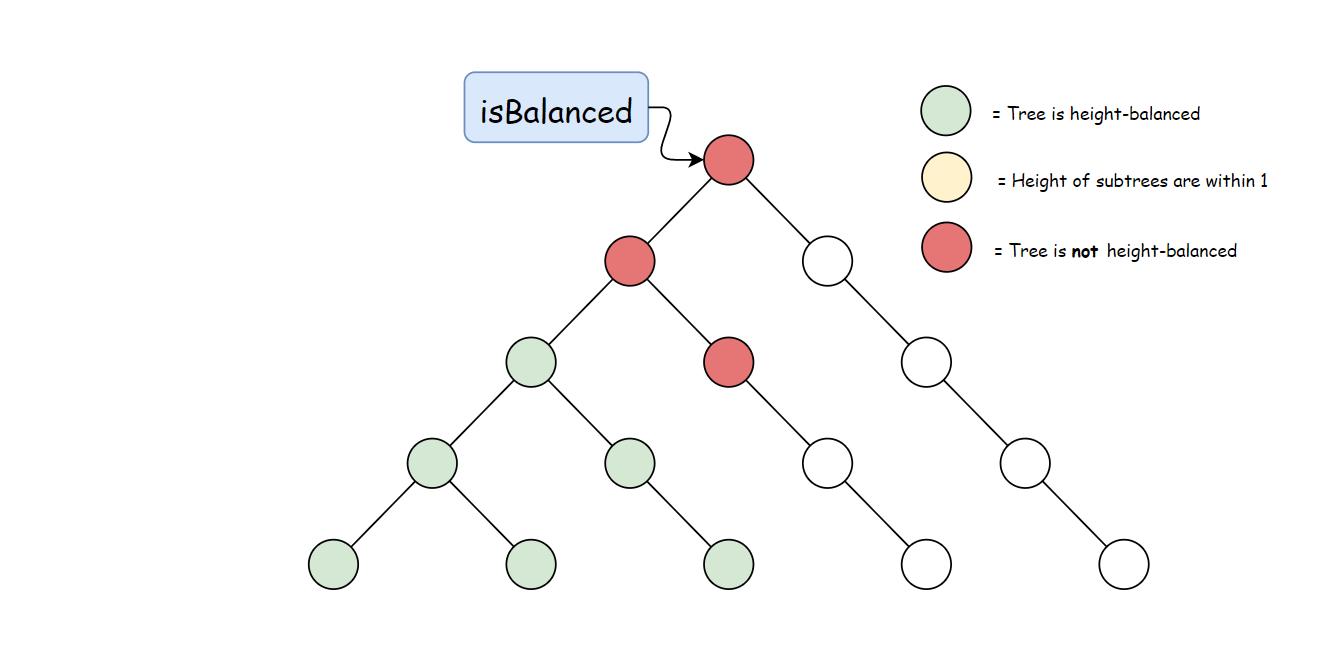
如何判断一棵二叉树是否是平衡二叉树.

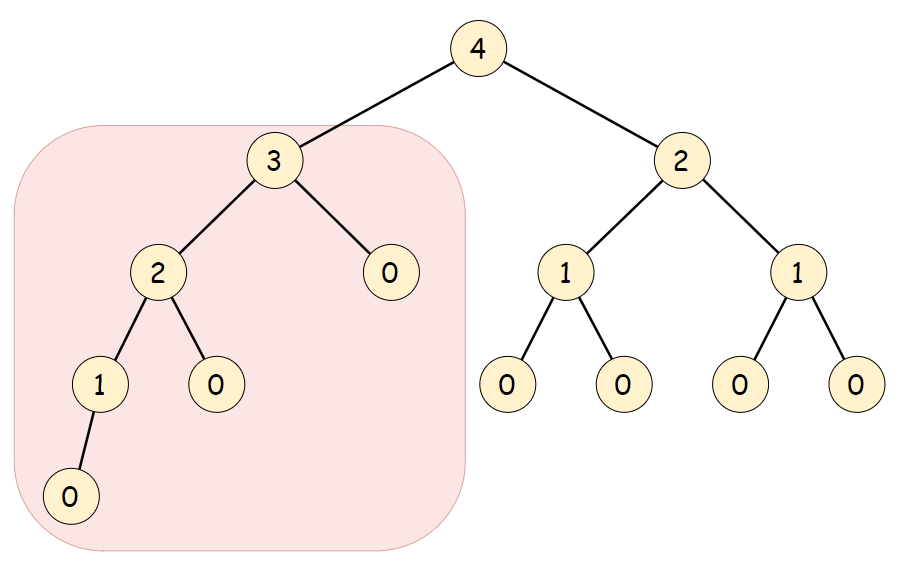
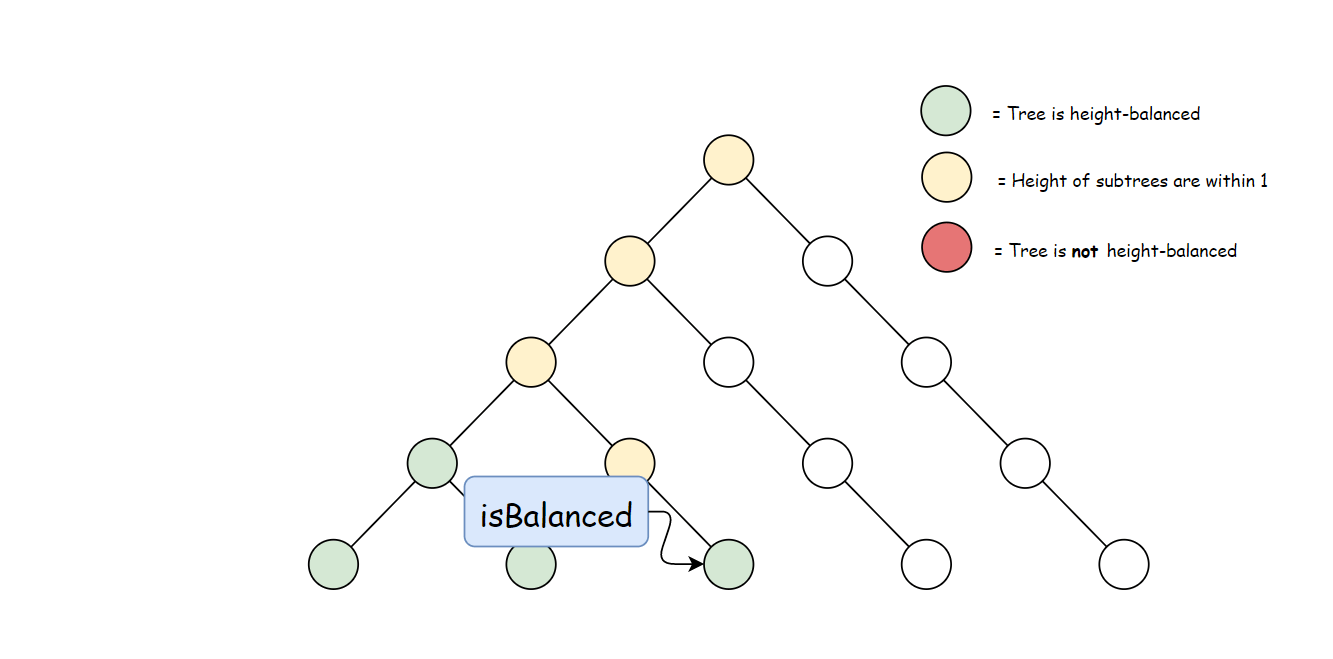
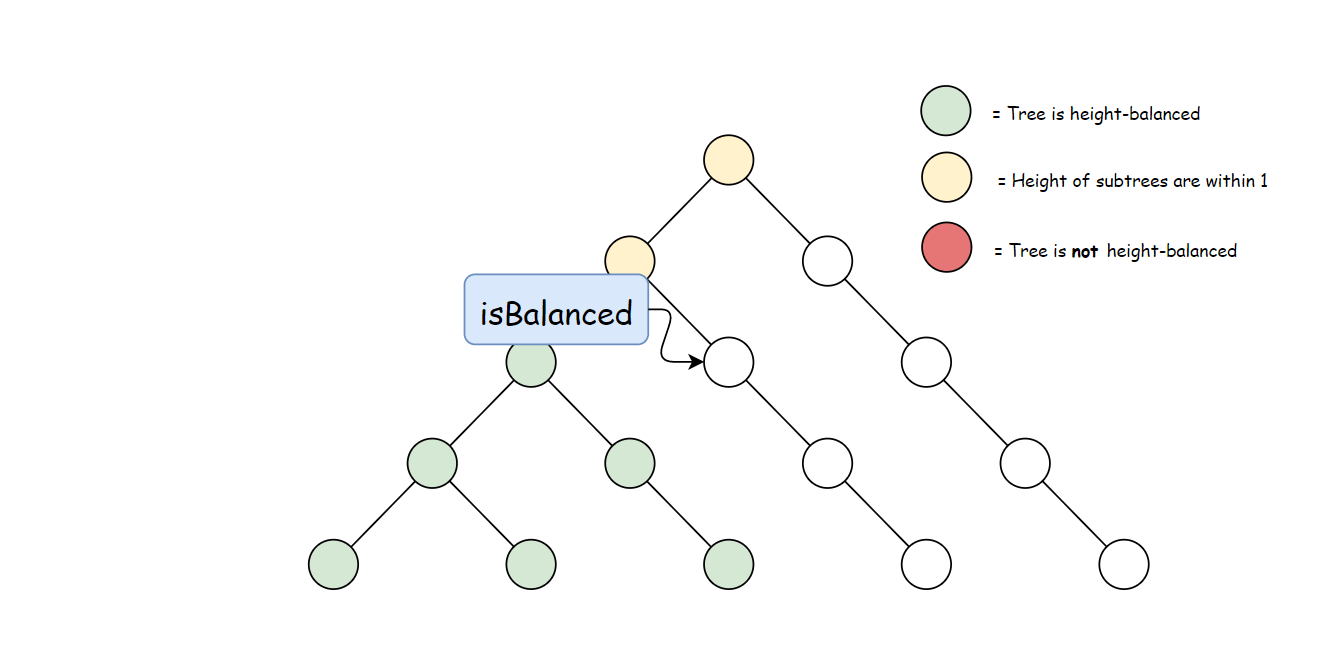
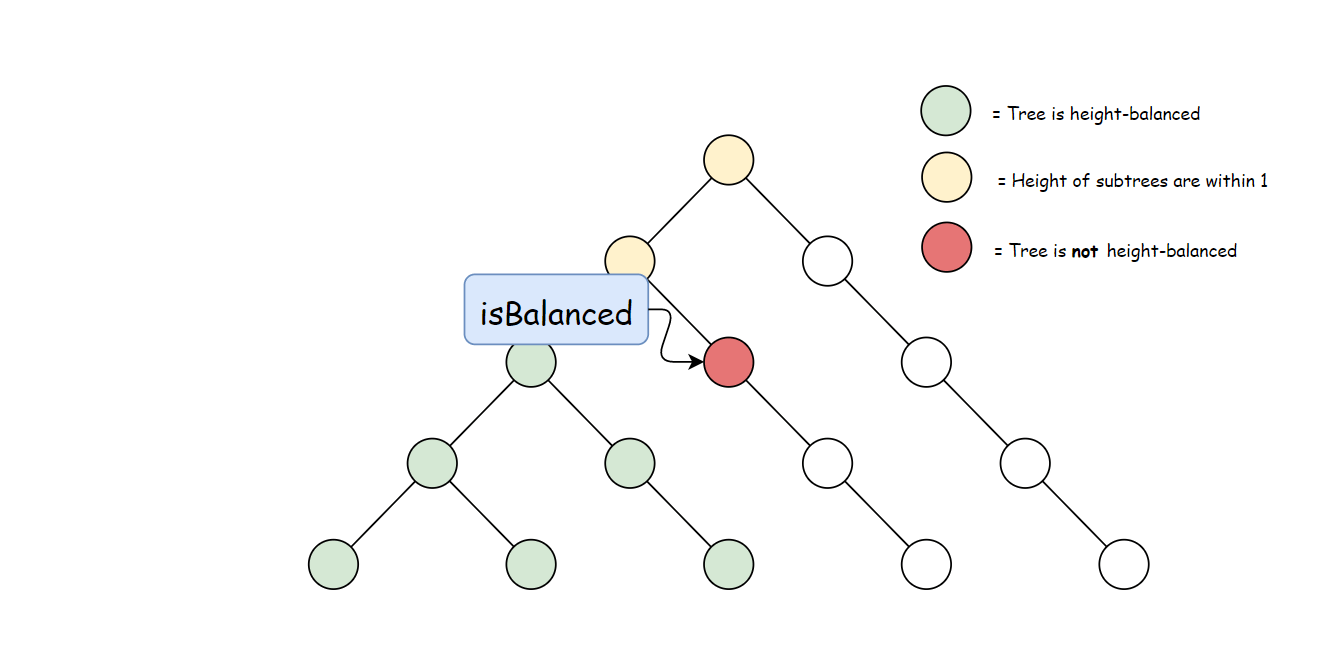
根据定义，一棵二叉树 T 存在节点 p∈T，满足 height(p.left)−height(p.right)>1 时，它是不平衡的。 下图中每个节点的高度都被标记出来，高亮区域是一棵不平衡子树。

平衡子树暗示了一个事实，每棵子树也是一个子问题。
现在的问题是：按照什么顺序处理这些子问题？

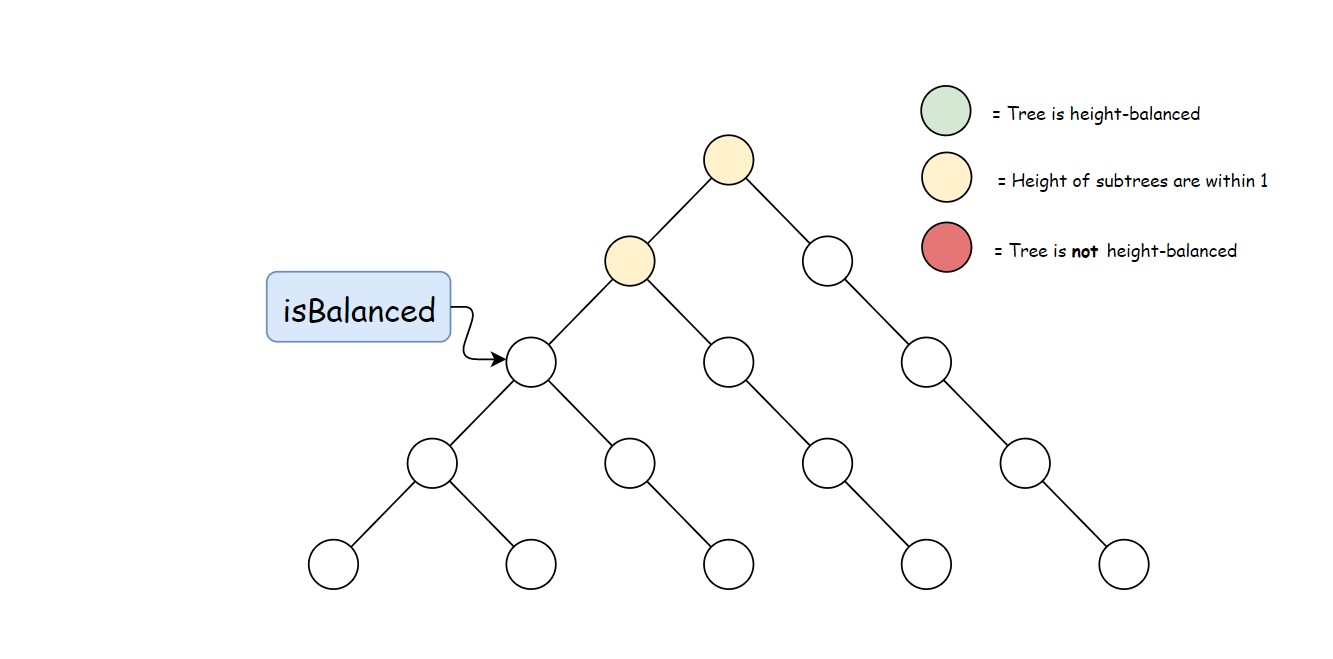
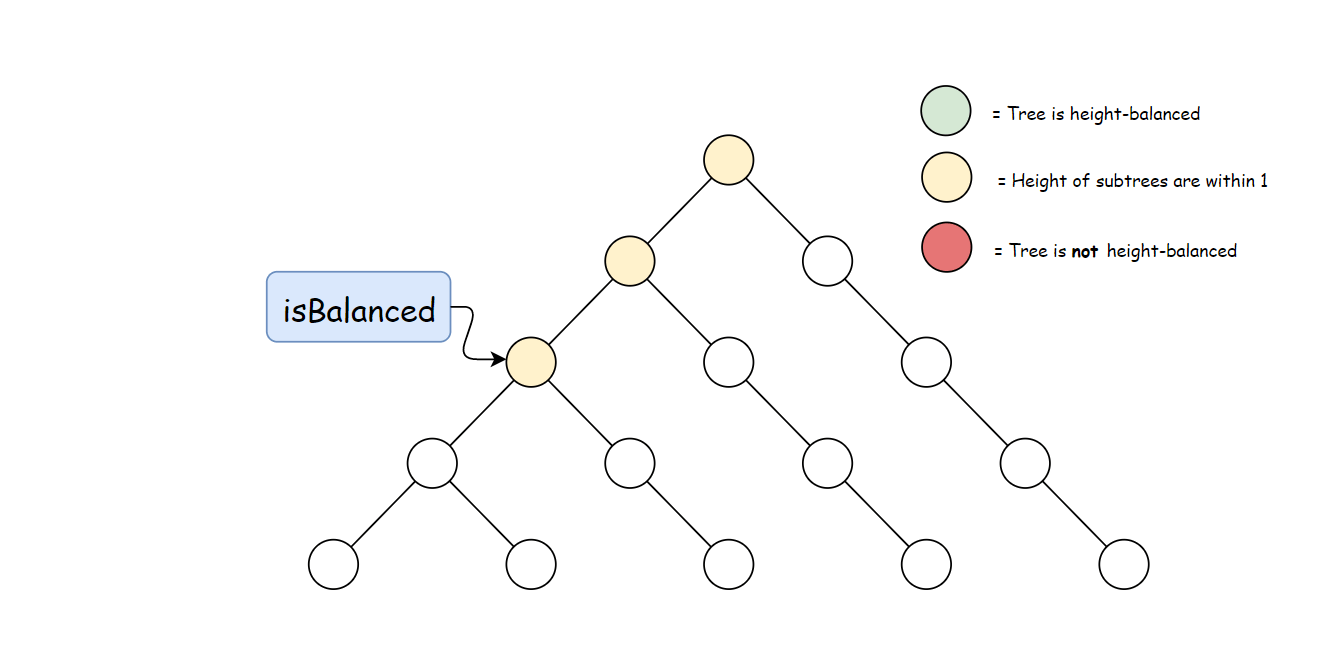
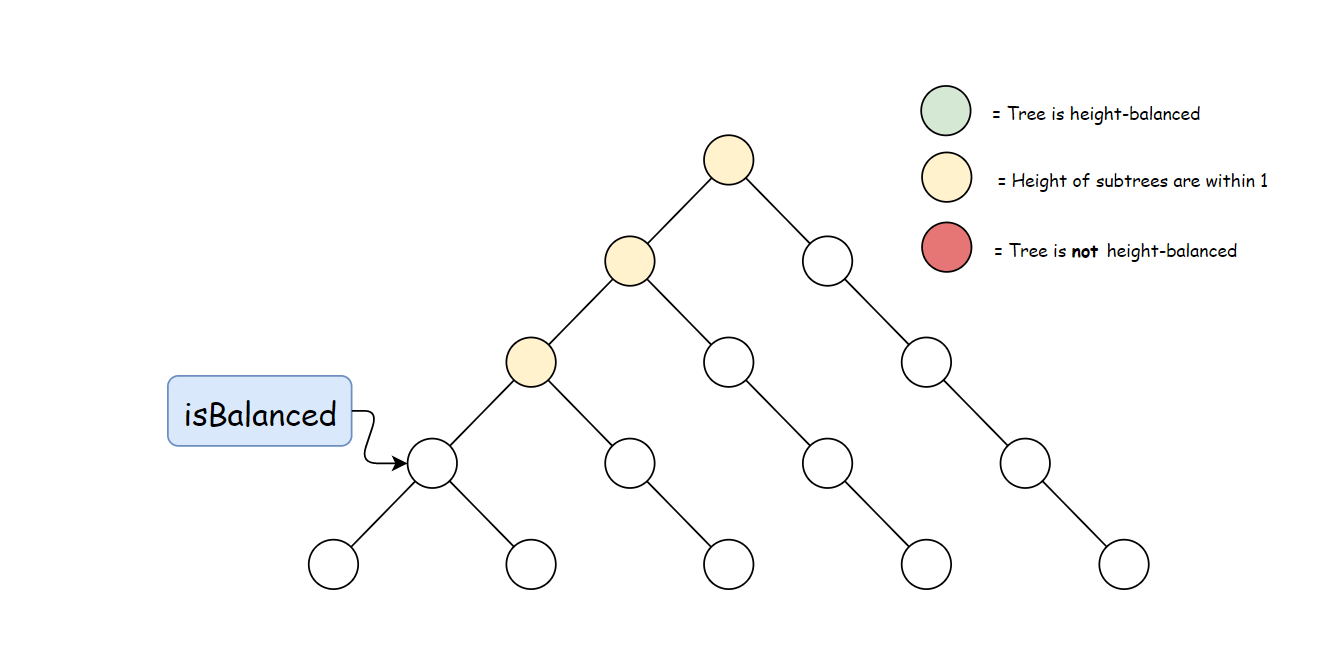
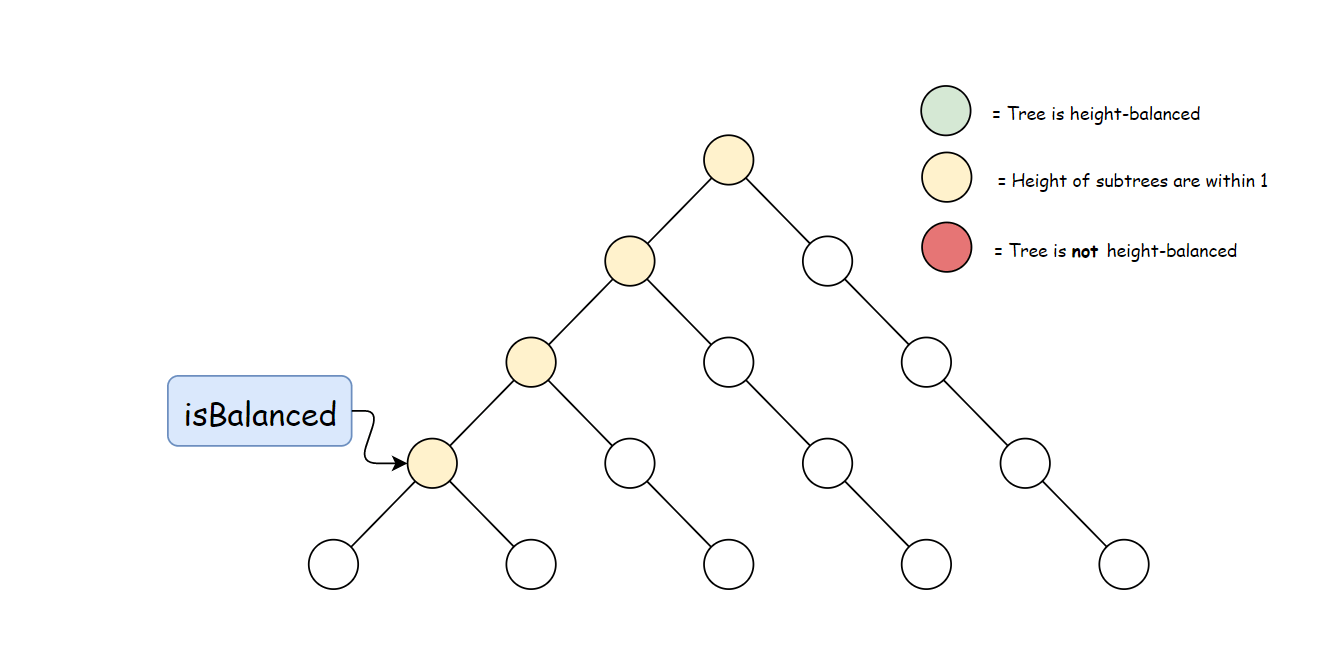
方法一：自顶向下的递归

定义方法 height，用于计算任意一个节点 p∈T 的高度：

接下来就是比较每个节点左右子树的高度。 在一棵以 rr 为根节点的树 TT 中，只有每个节点左右子树高度差不大于 1 时，该树才是平衡的。因此可以比较每个节点左右两棵子树的高度差，然后向上递归。

class Solution {
  // Recursively obtain the height of a tree. An empty tree has -1 height
  private int height(TreeNode root) {
    // An empty tree has height -1
    if (root == null) {
      return -1;
    }
    return 1 + Math.max(height(root.left), height(root.right));
  }

  public boolean isBalanced(TreeNode root) {
    // An empty tree satisfies the definition of a balanced tree
    if (root == null) {
      return true;
    }

    // Check if subtrees have height within 1. If they do, check if the
    // subtrees are balanced
    return Math.abs(height(root.left) - height(root.right)) < 2
        && isBalanced(root.left)
        && isBalanced(root.right);
  }
};

复杂度分析

• 时间复杂度：O(nlogn)。

  对于每个深度为 d 的节点 p，height(p) 被调用 p 次。 首先，需要知道一棵平衡二叉树可以拥有的节点数量。令 f(h) 表示一棵高度为 h 的平衡二叉树需要的最少节点数量。

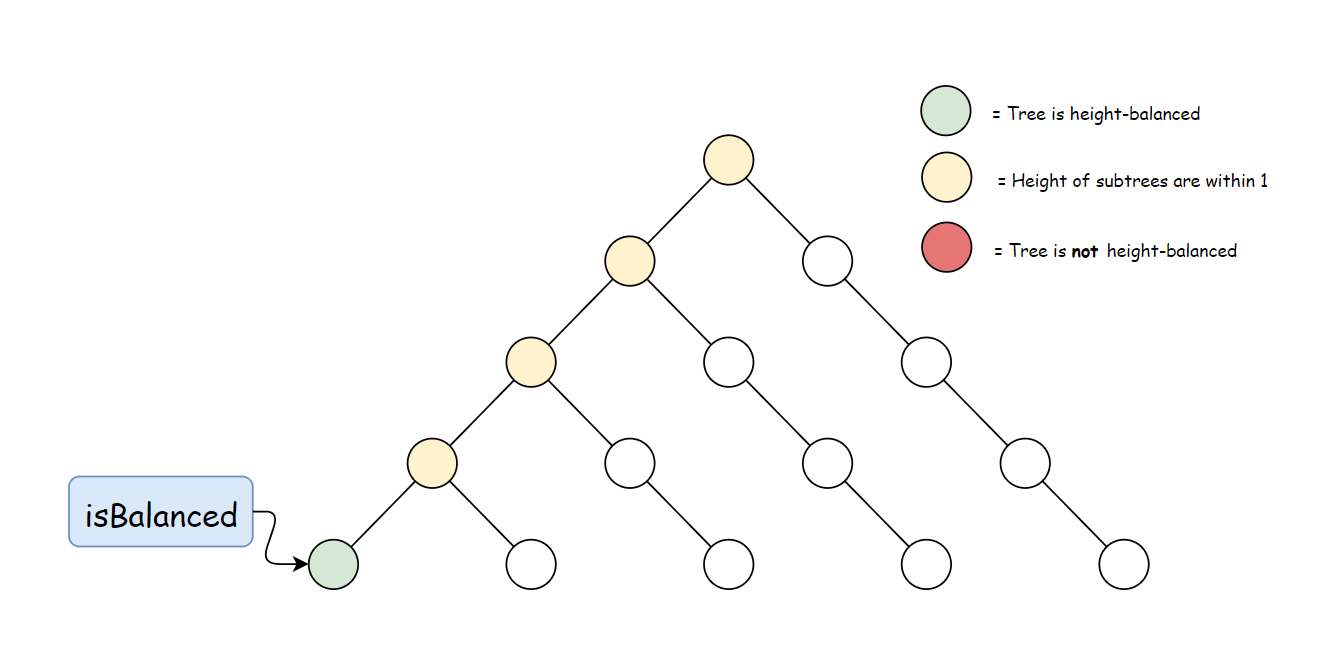
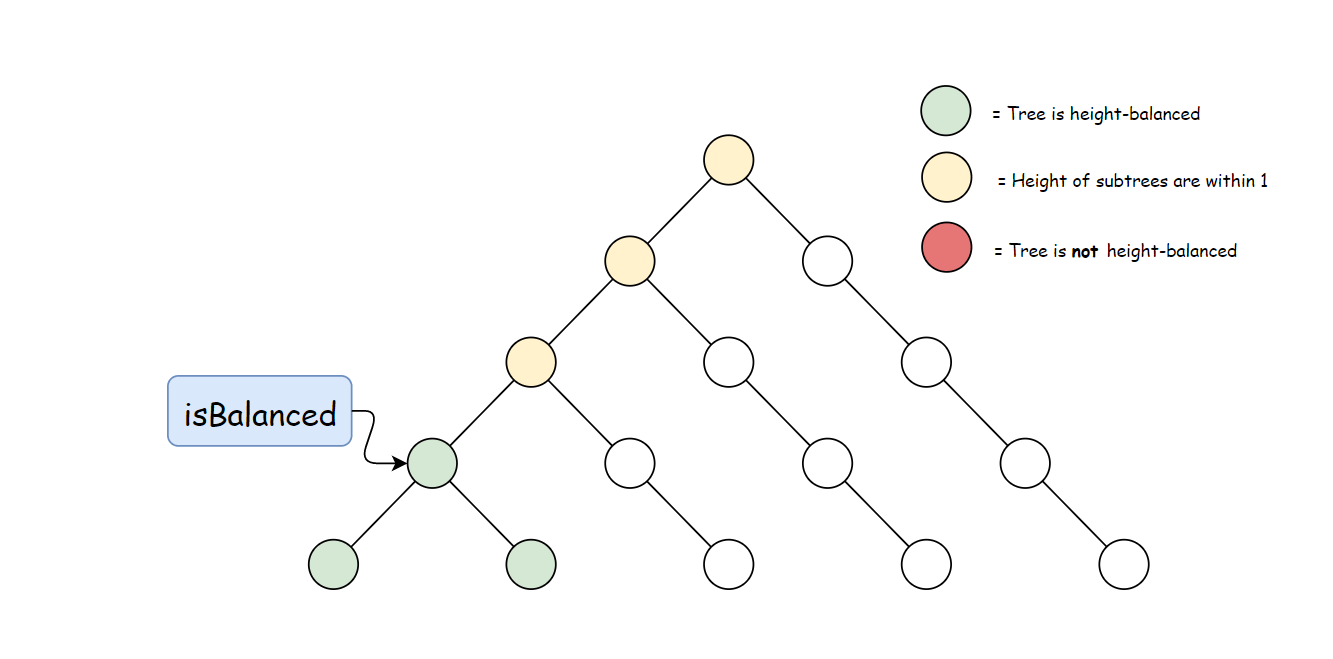
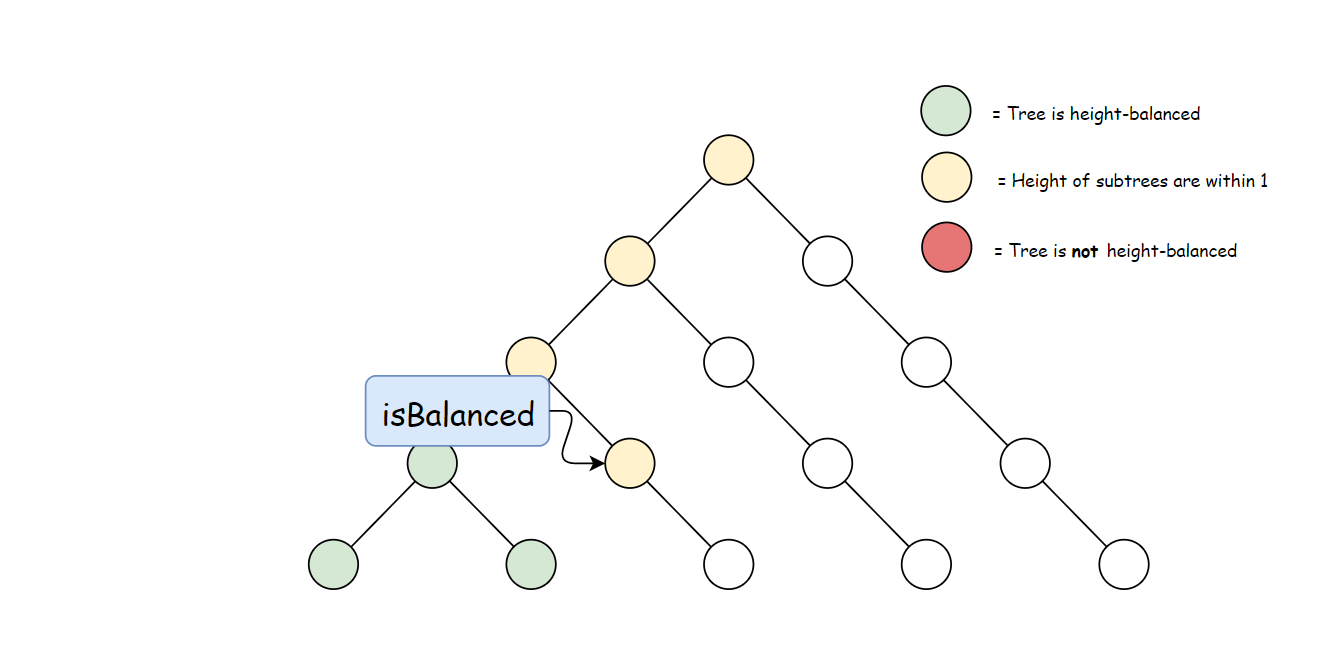
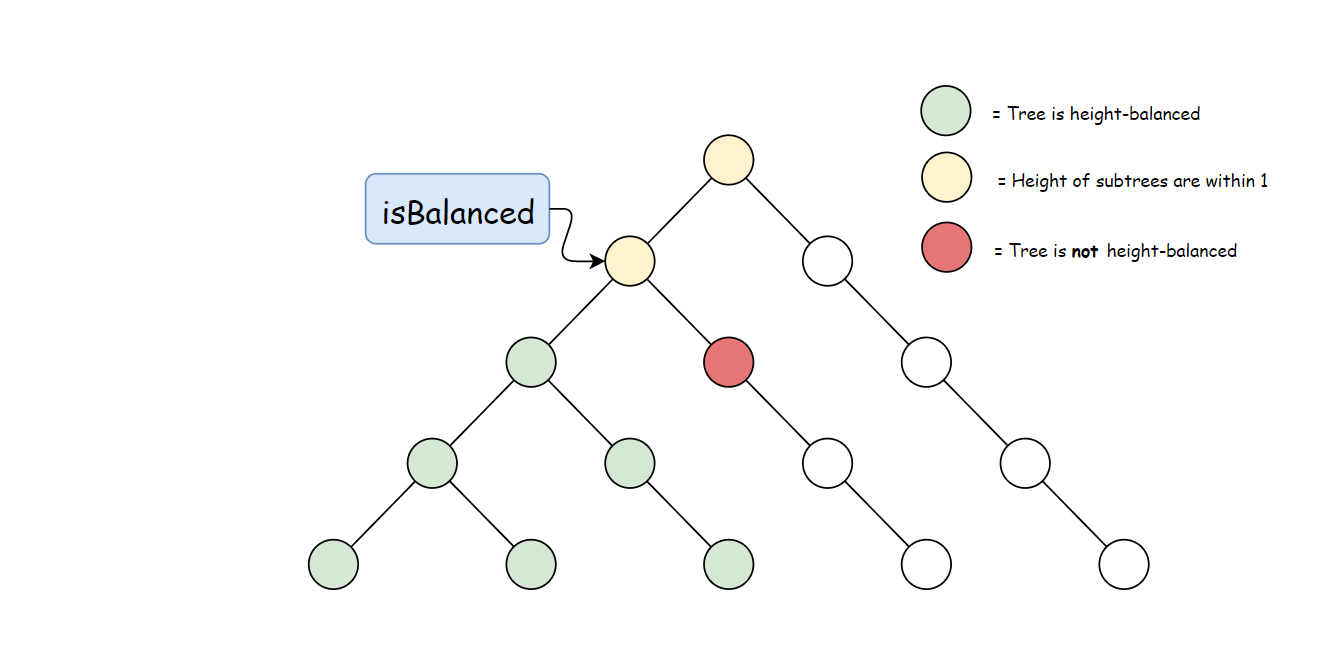
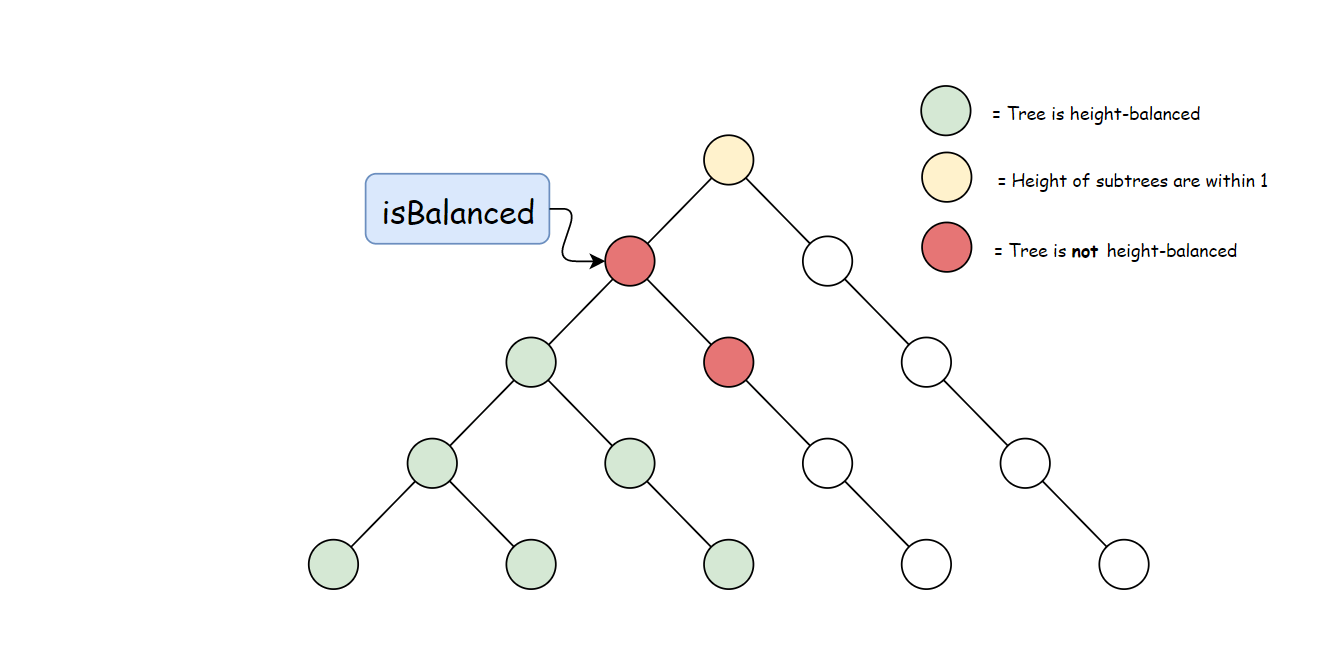
方法二：自底向上的递归

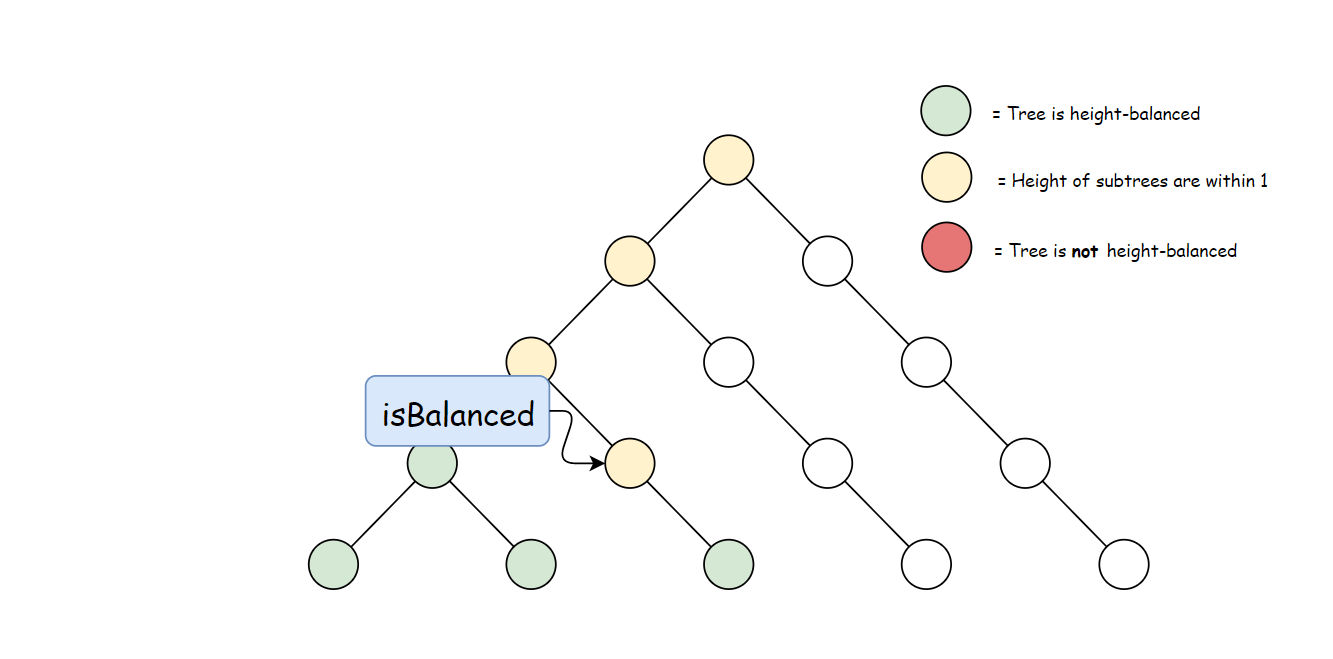
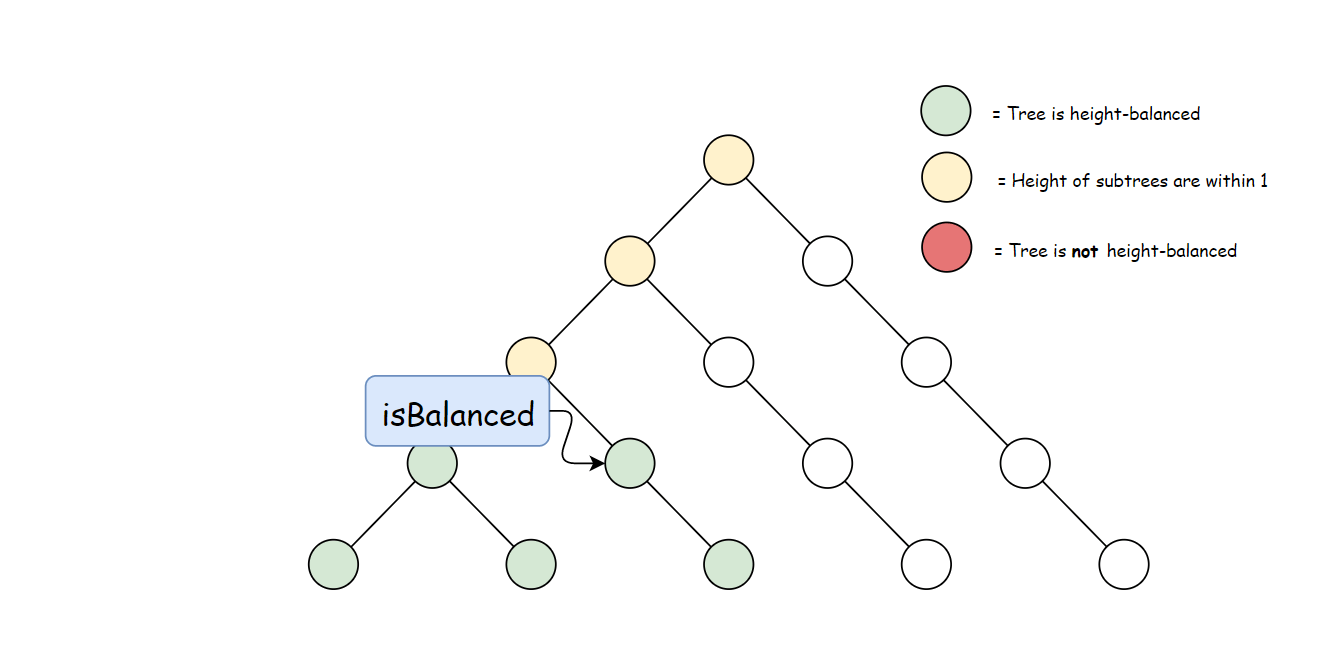
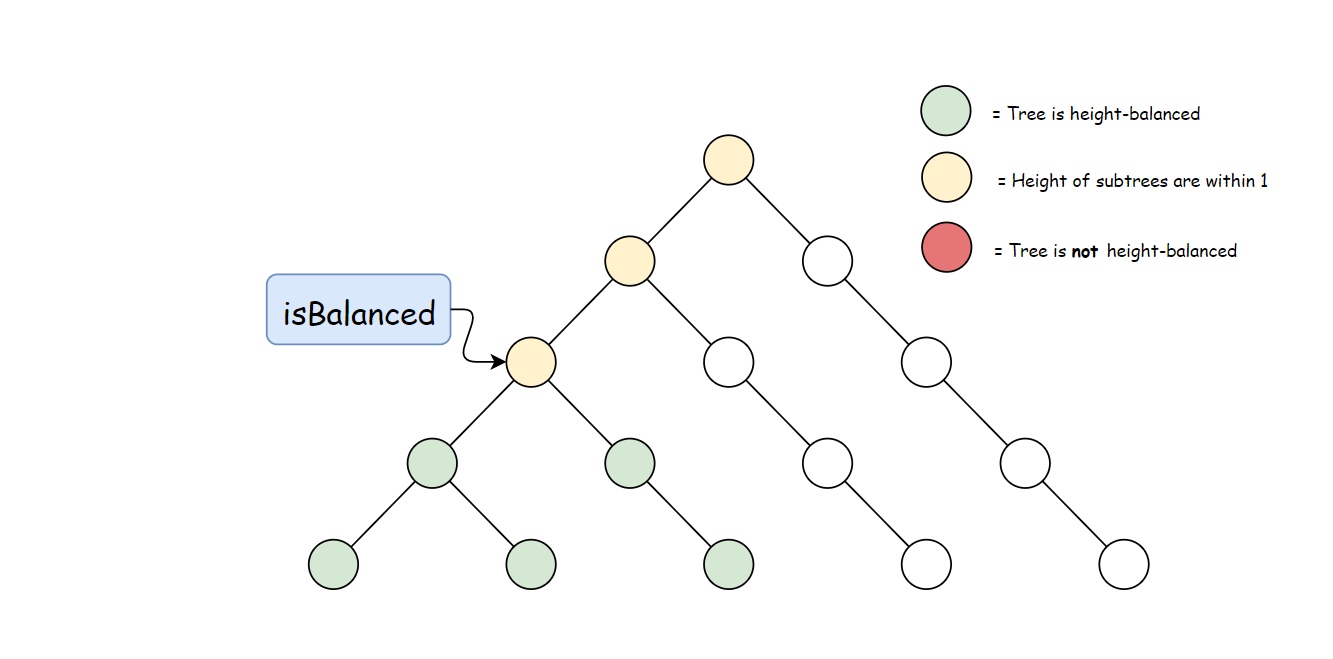
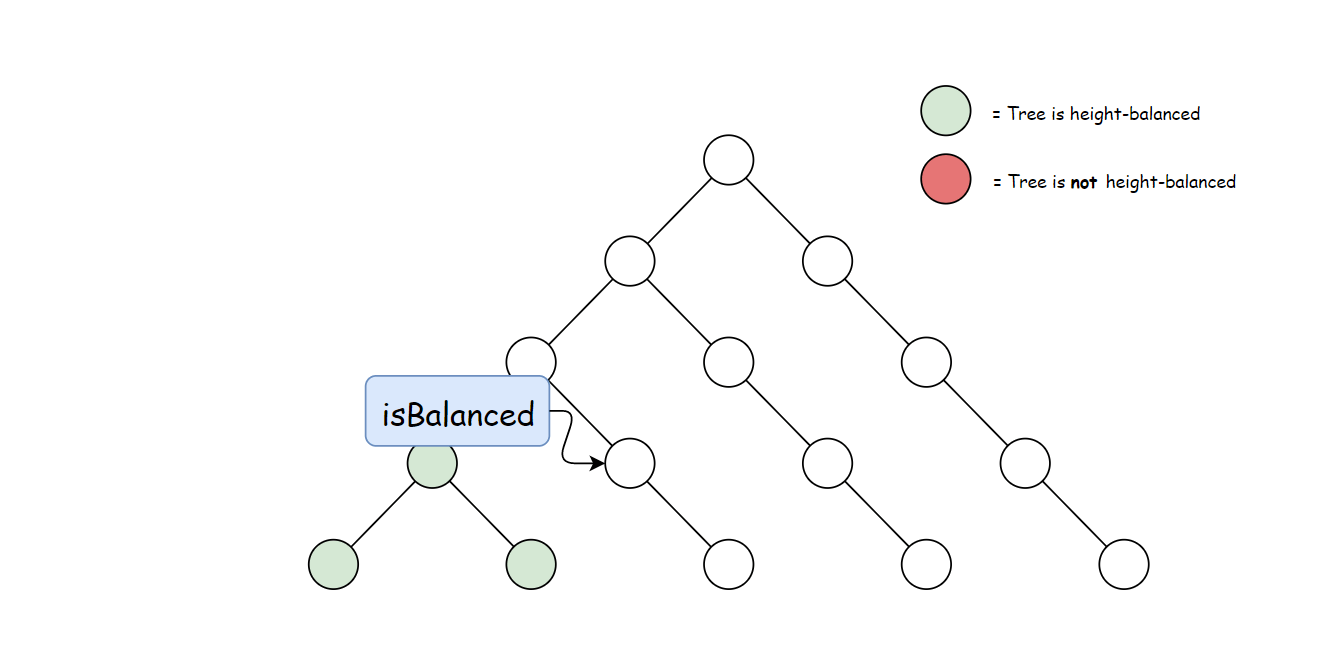
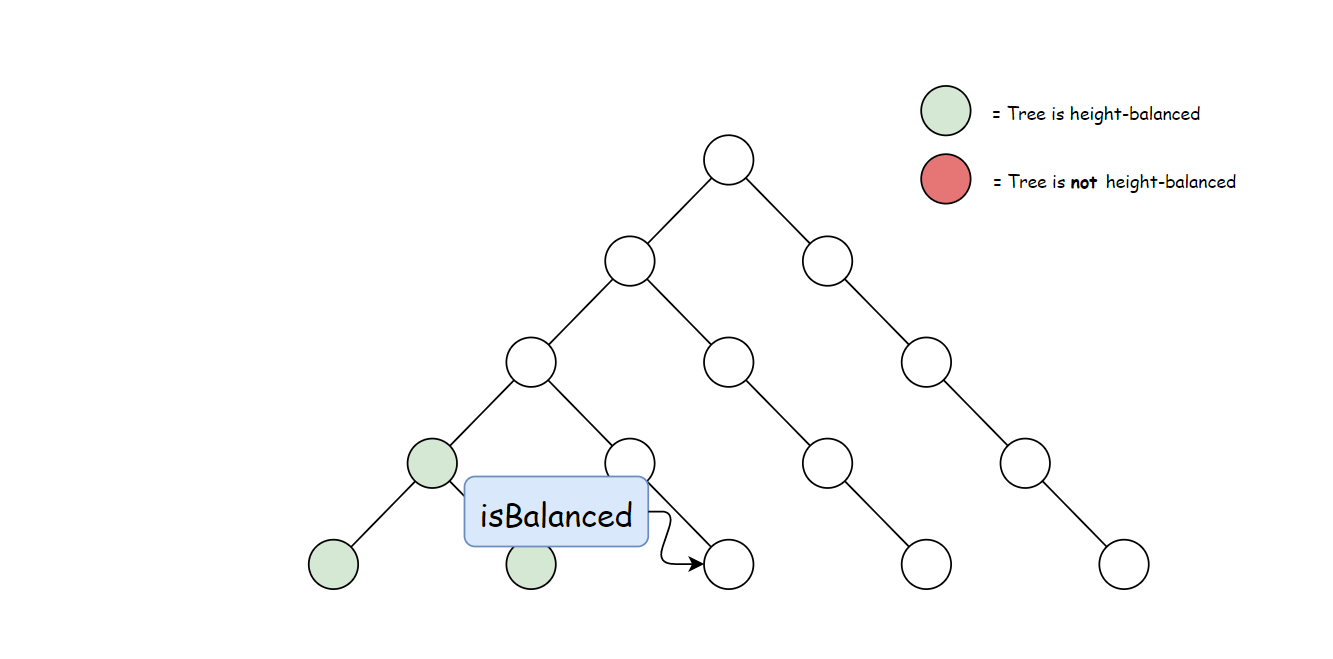
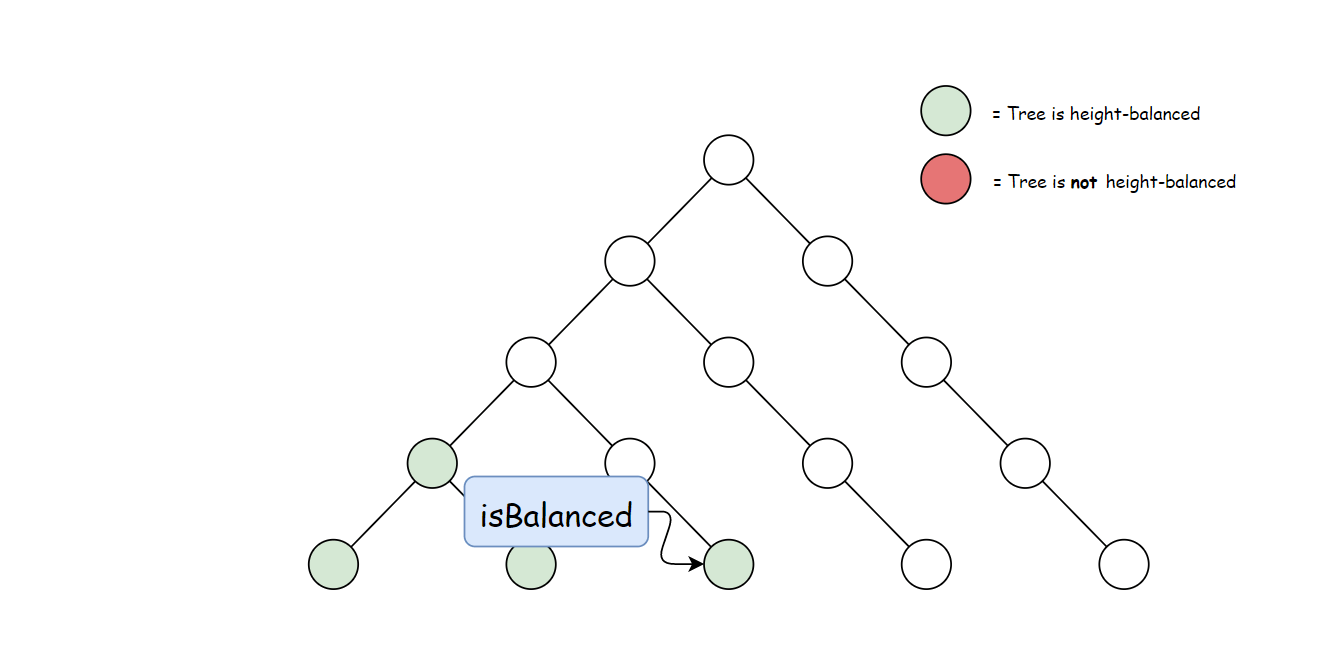
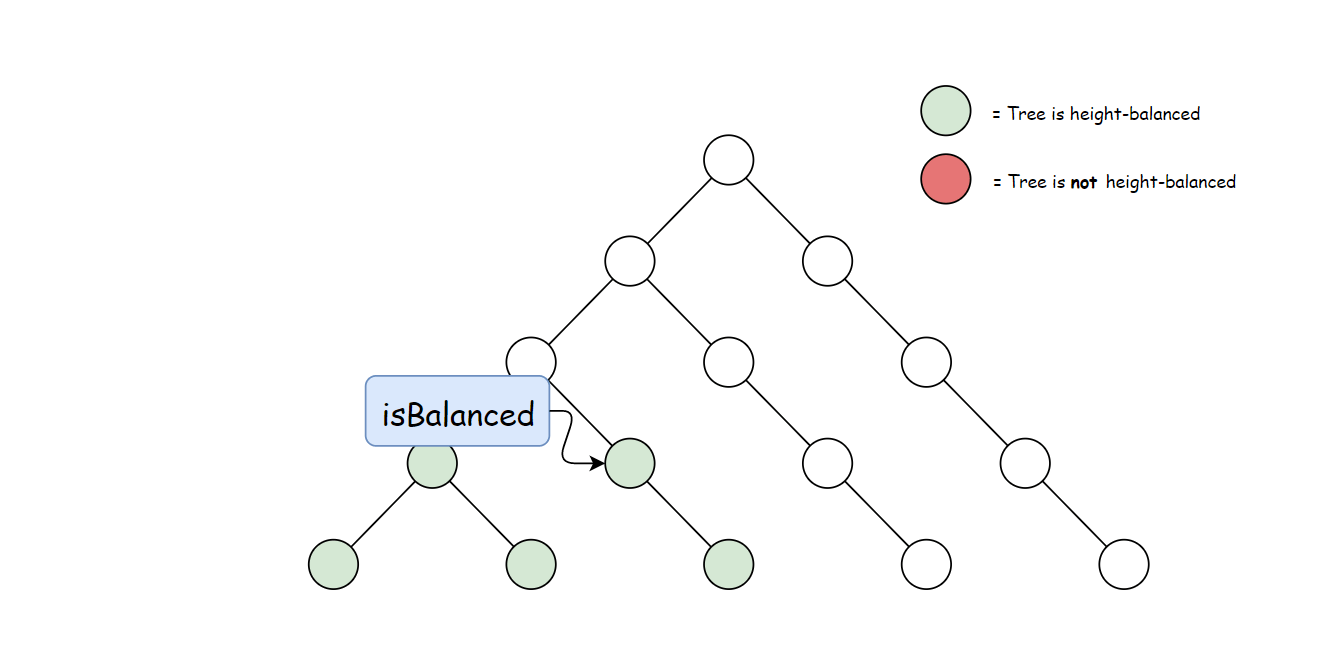
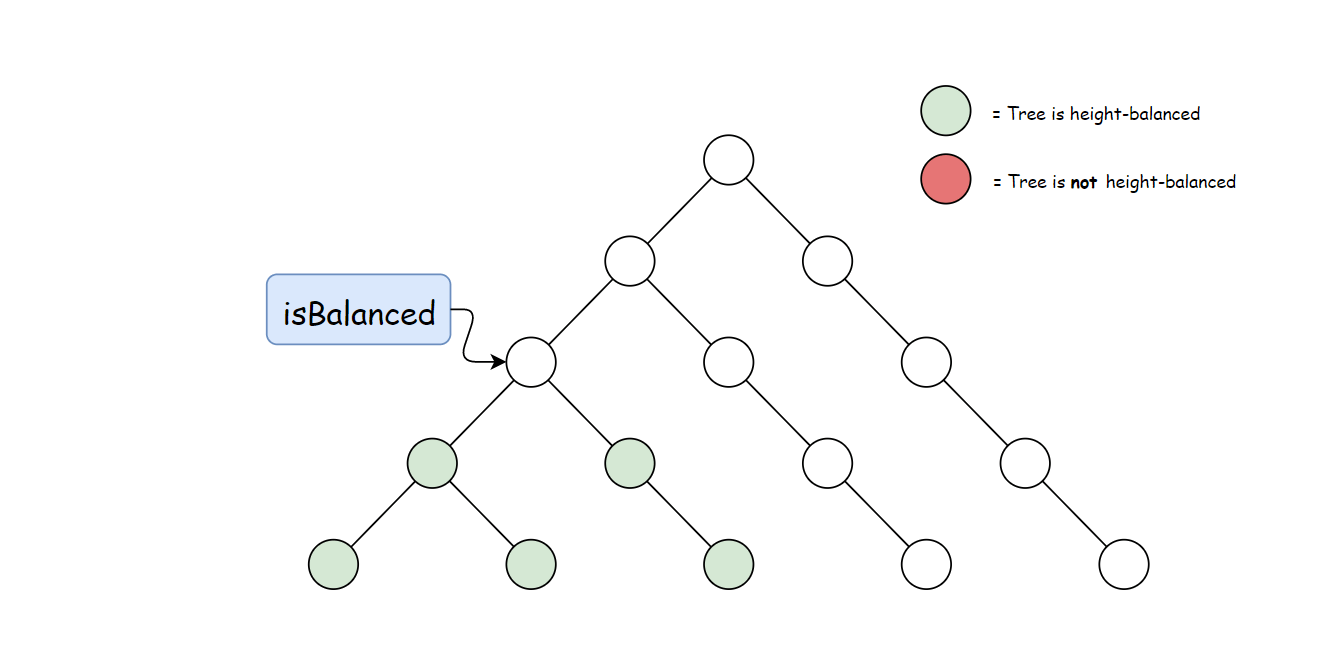
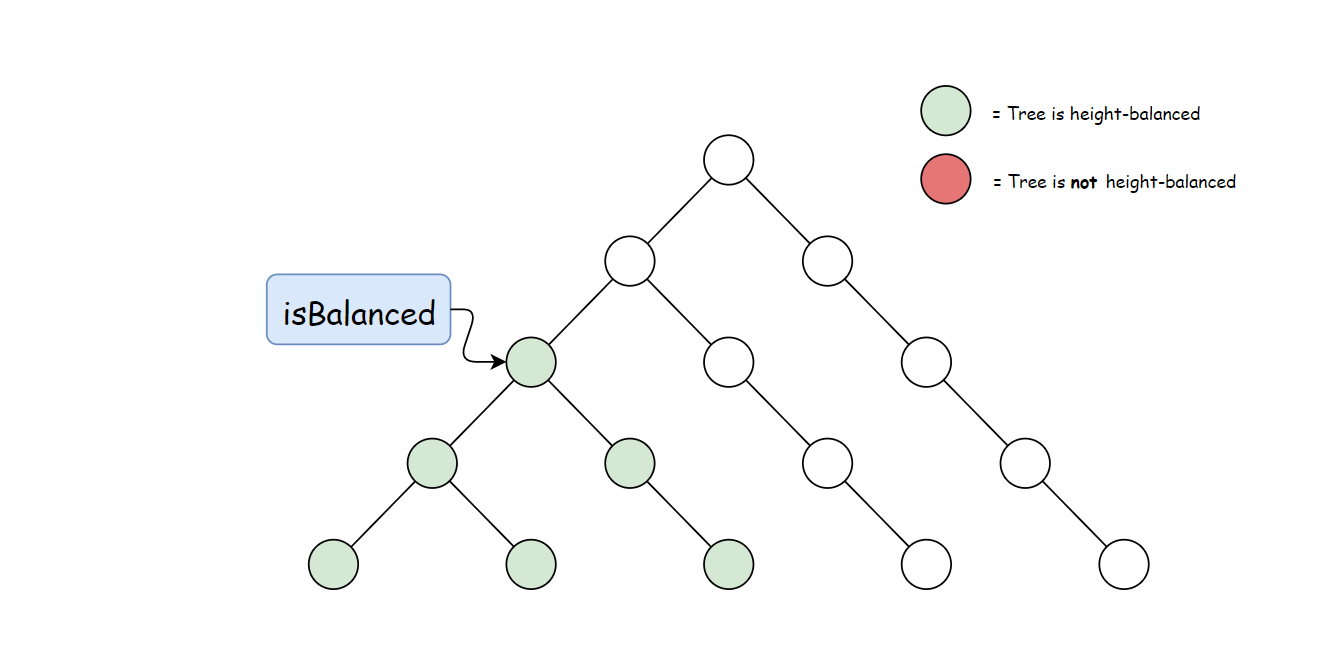
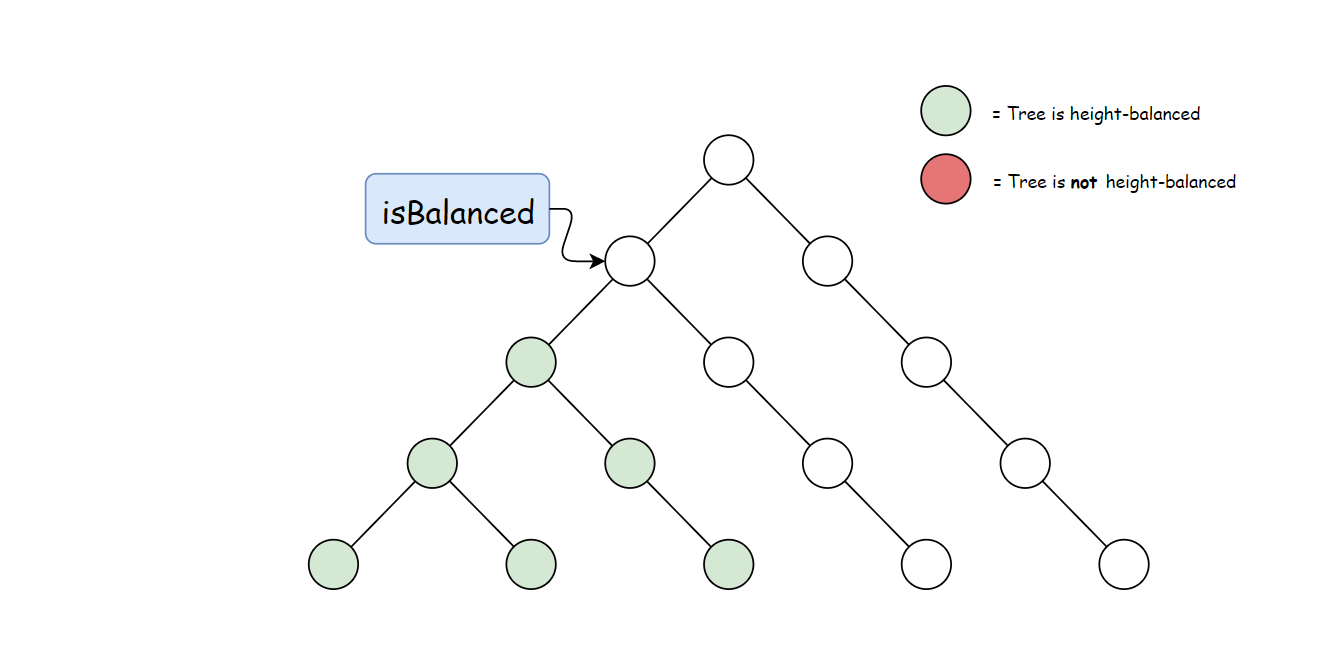
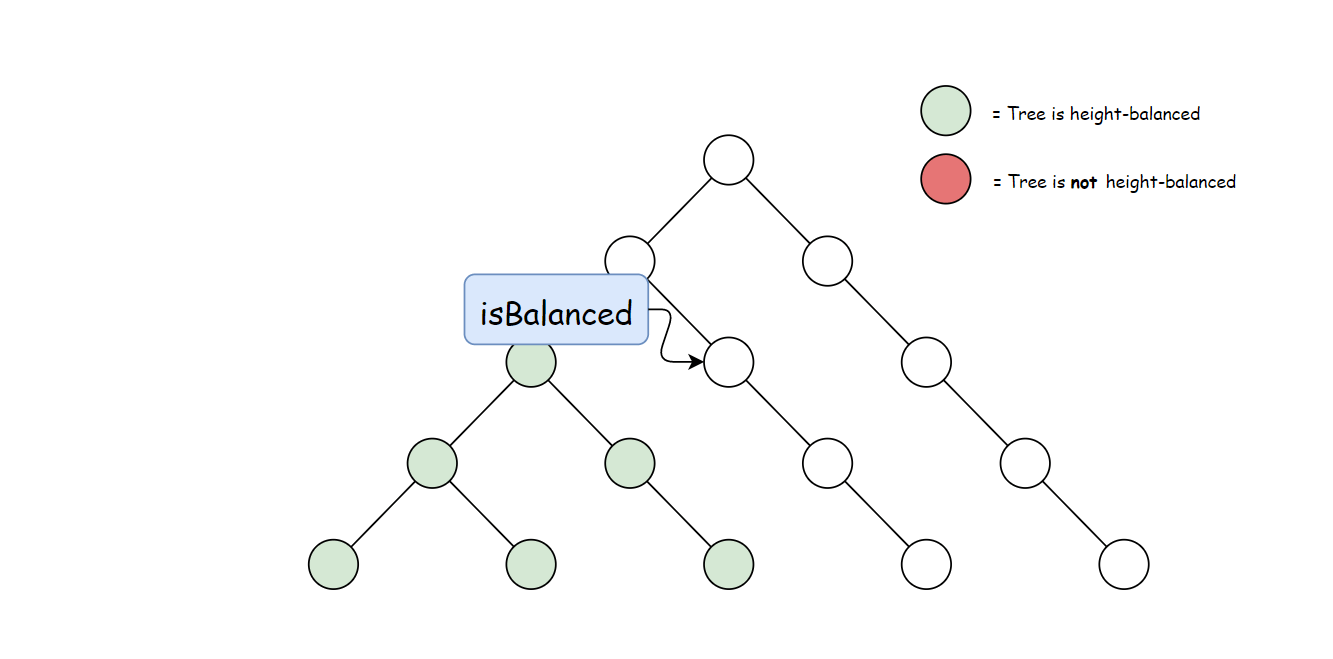
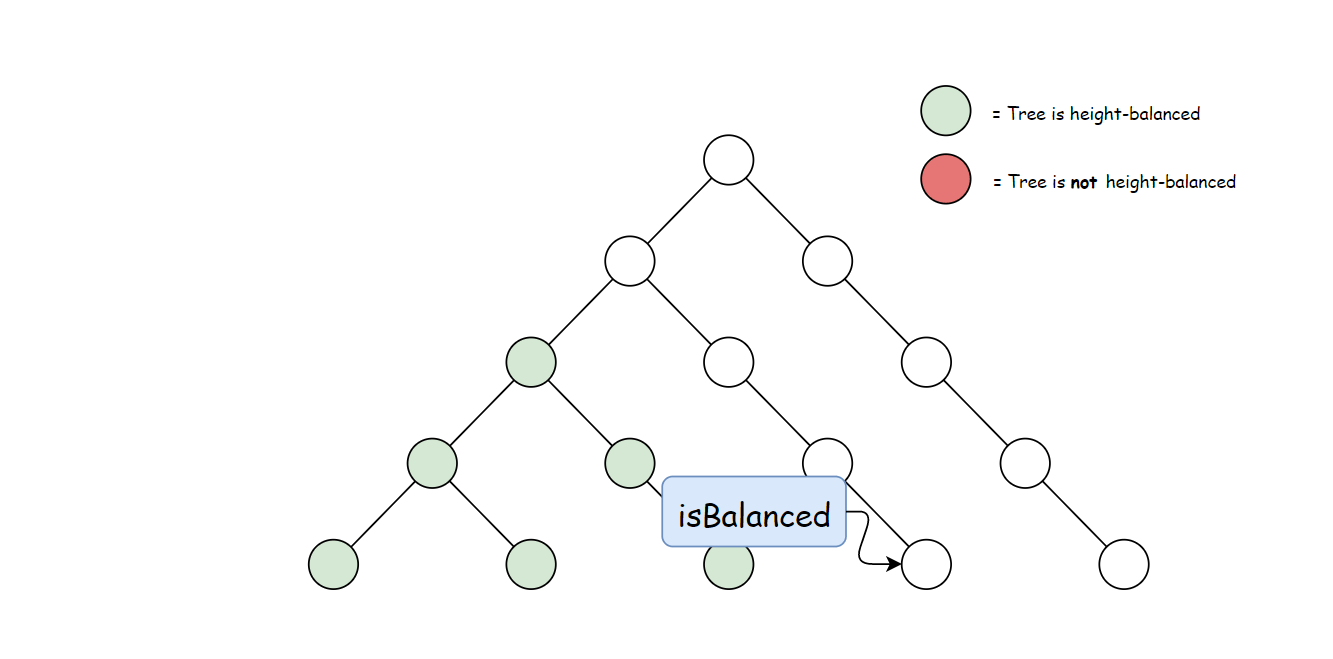
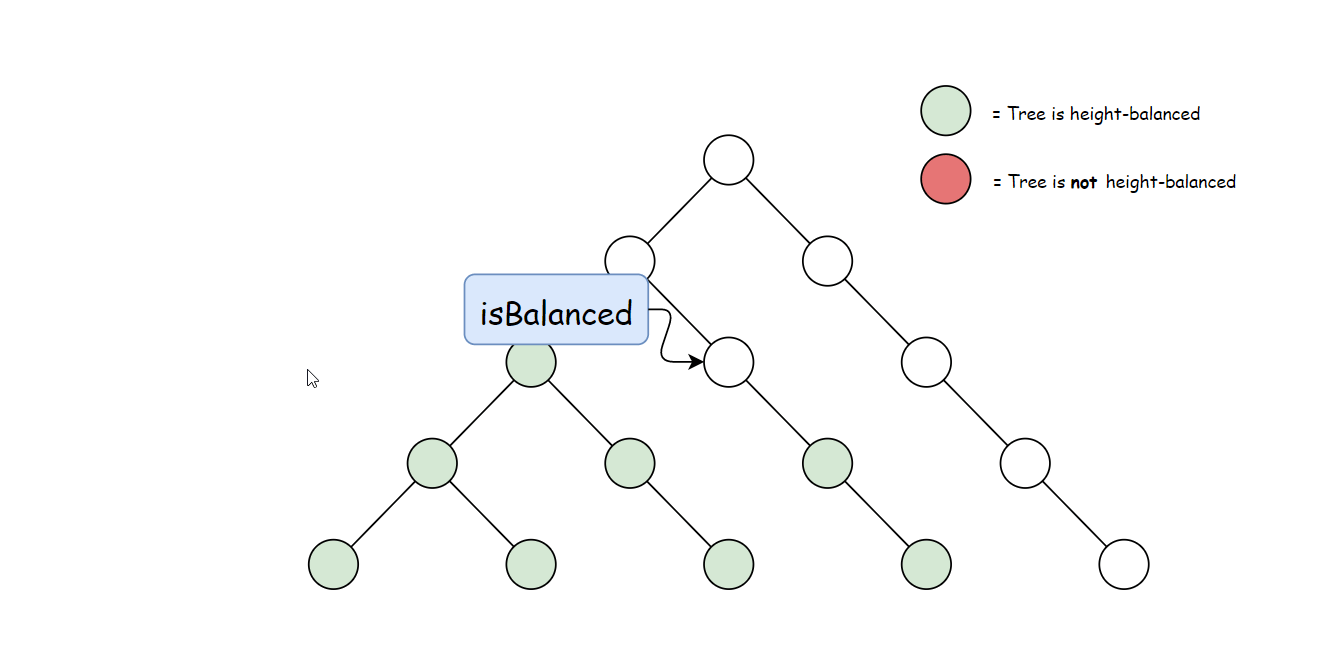
方法一计算 height 存在大量冗余。 每次调用 height 时，要同时计算其子树高度。 但是自底向上计算，每个子树的高度只会计算一次。 可以递归先计算当前节点的子节点高度， 然后再通过子节点高度判断当前节点是否平衡，从而消除冗余。

算法

使用与方法一中定义的 height 方法。 自底向上与自顶向下的逻辑相反，首先判断子树是否平衡， 然后比较子树高度判断父节点是否平衡。算法如下：

// Utility class to store information from recursive calls
final class TreeInfo {
  public final int height;
  public final boolean balanced;

  public TreeInfo(int height, boolean balanced) {
    this.height = height;
    this.balanced = balanced;
  }
}

class Solution {
  // Return whether or not the tree at root is balanced while also storing
  // the tree's height in a reference variable.
  private TreeInfo isBalancedTreeHelper(TreeNode root) {
    // An empty tree is balanced and has height = -1
    if (root == null) {
      return new TreeInfo(-1, true);
    }

    // Check subtrees to see if they are balanced.
    TreeInfo left = isBalancedTreeHelper(root.left);
    if (!left.balanced) {
      return new TreeInfo(-1, false);
    }
    TreeInfo right = isBalancedTreeHelper(root.right);
    if (!right.balanced) {
      return new TreeInfo(-1, false);
    }

    // Use the height obtained from the recursive calls to
    // determine if the current node is also balanced.
    if (Math.abs(left.height - right.height) < 2) {
      return new TreeInfo(Math.max(left.height, right.height) + 1, true);
    }
    return new TreeInfo(-1, false);
  }

  public boolean isBalanced(TreeNode root) {
    return isBalancedTreeHelper(root).balanced;
  }
};

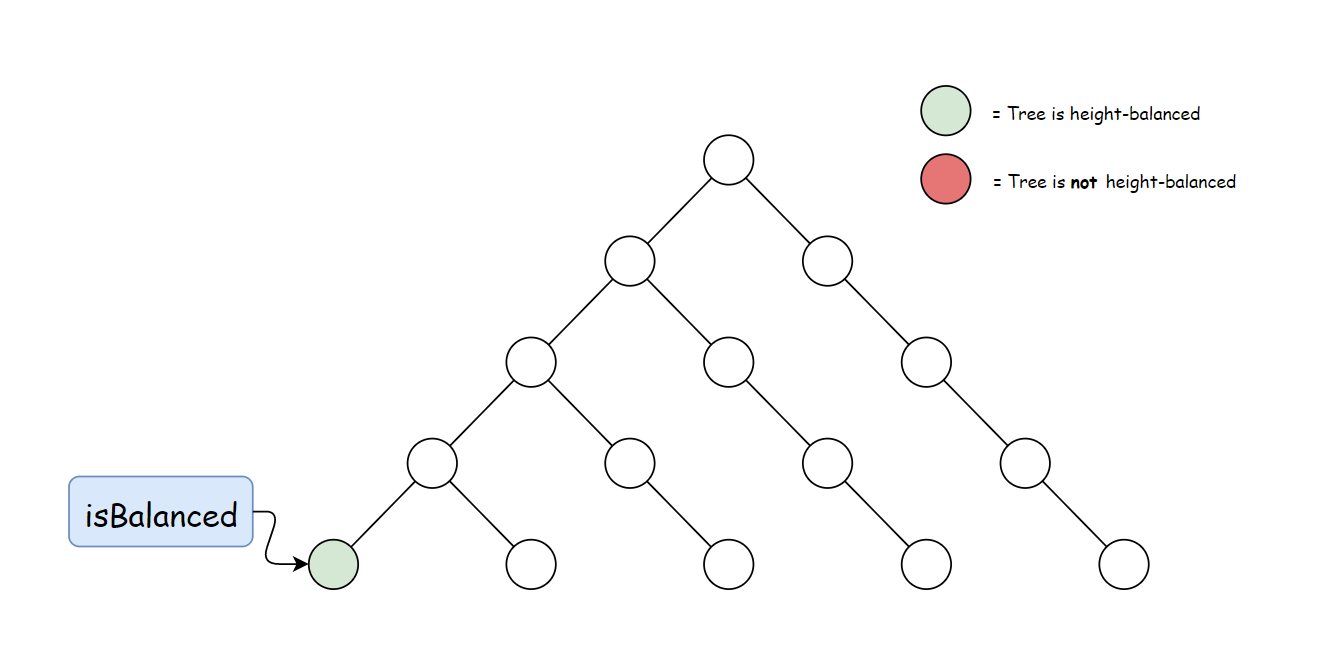
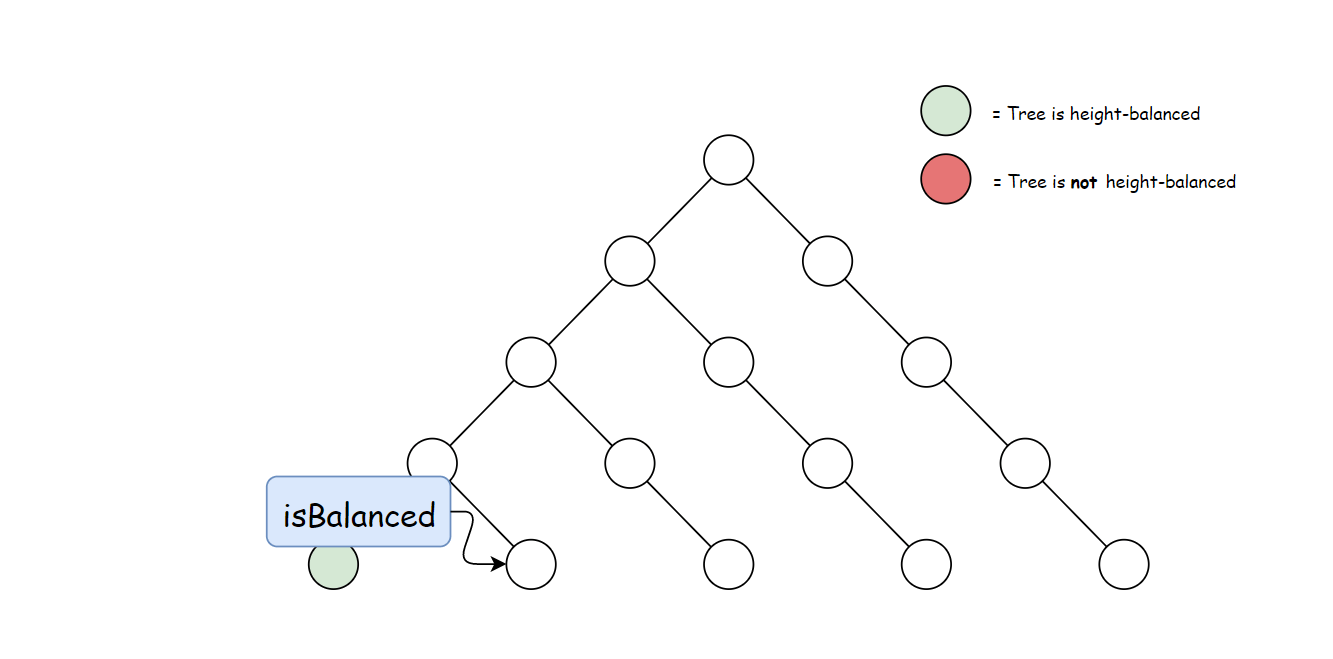
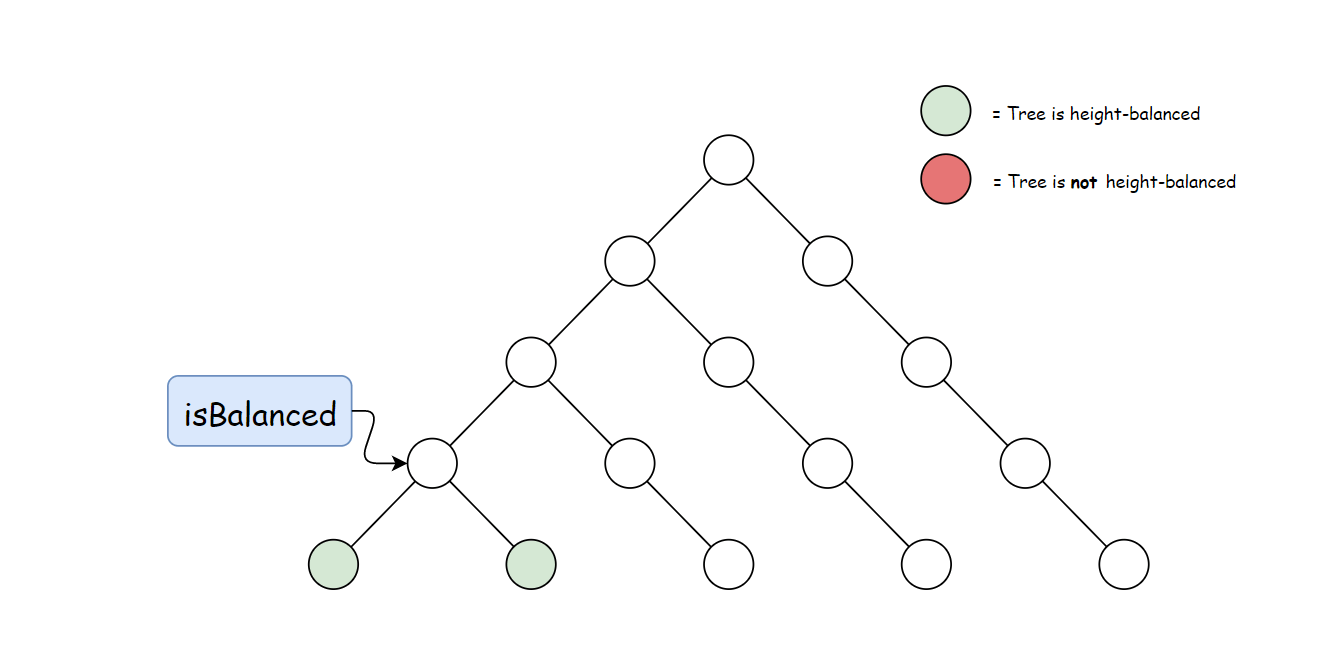
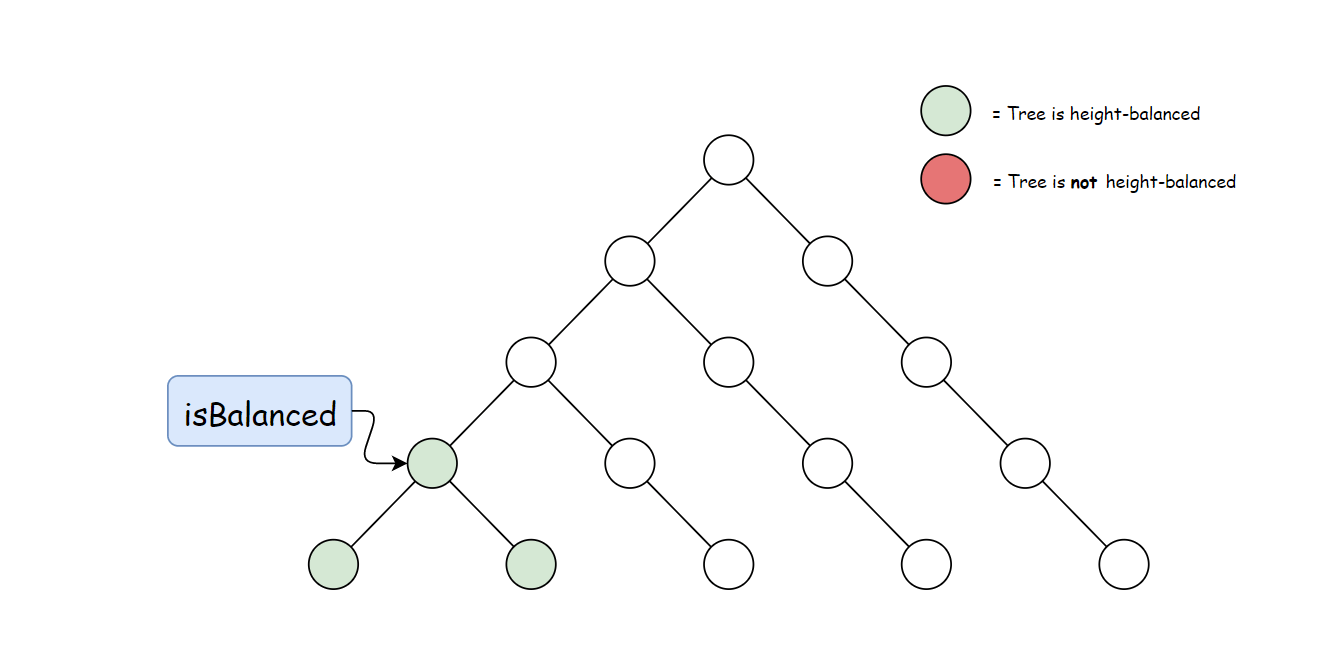
复杂度分析

时间复杂度：O(n)，计算每棵子树的高度和判断平衡操作都在恒定时间内完成。

空间复杂度：O(n)，如果树不平衡，递归栈可能达到 O(n)。

https://leetcode-cn.com/problems/balanced-binary-tree/

拓展：判断一棵树是否平衡

实现一个函数检查一棵树是否平衡。对于这个问题而言， 平衡指的是这棵树任意两个叶子结点到根结点的距离之差不大于1。

对于这道题，要审清题意。它并不是让你判断一棵树是否为平衡二叉树。

平衡二叉树的定义为：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

而本题的平衡指的是这棵树任意两个叶子结点到根结点的距离之差不大于1。 这两个概念是不一样的。例如下图，

它是一棵平衡二叉树，但不满足本题的平衡条件。 (叶子结点f和l到根结点的距离之差等于2，不满足题目条件)

对于本题，只需要求出离根结点最近和最远的叶子结点， 然后看它们到根结点的距离之差是否大于1即可。

假设只考虑二叉树，我们可以通过遍历一遍二叉树求出每个叶子结点到根结点的距离。 使用中序遍历，依次求出从左到右的叶子结点到根结点的距离，递归实现。

/*判断树是否平衡，并不是判断是否是平衡二叉树*/

int Max=INT_MIN,Min=INT_MAX,curLen=0;

void FindDepth(node* root)
{
    if( root==NULL) 
    {
        return ;
    }
    ++curLen;
    FindDepth(root->left);
    if( root->left ==NULL && root->right ==NULL)
    {
        if( curLen > Max )
            Max=curLen;
        else if( curLen < Min )
            Min=curLen;
    }
    FindDepth(root->right);
    --curLen;
}
bool isBalance(node* root)
{
    FindDepth(root);
    return ((Max-Min)<=1);
}