树和森林与二叉树的相互转换
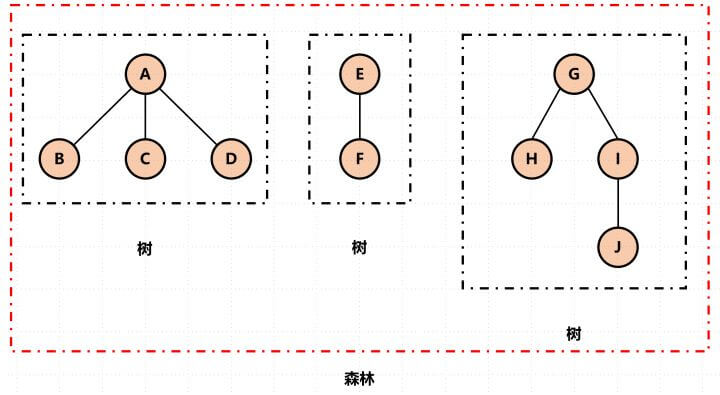
什么是森林?
很容易想到,由树组成森林。
专业一点的定义是:若干棵互不相交的树的集合。
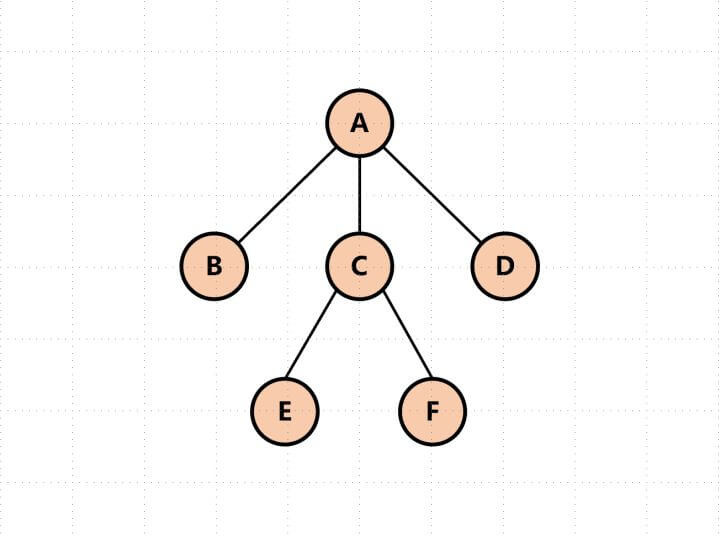
下面我们要用的是左孩子右兄弟的方法,
简单三步就能将树和二叉树相互转换。
树 -> 二叉树
加线。在所有的兄弟结点之间加一条线。
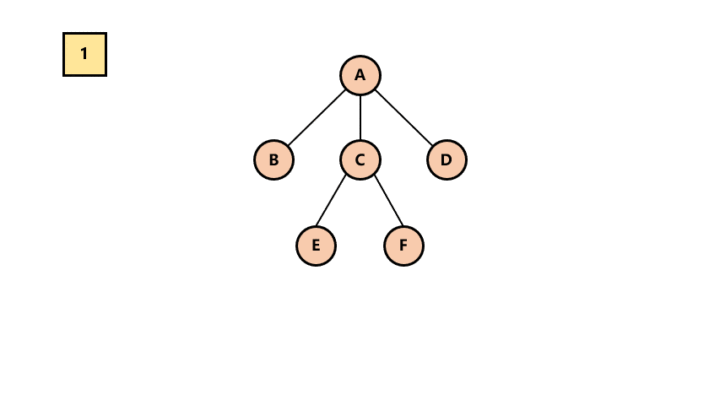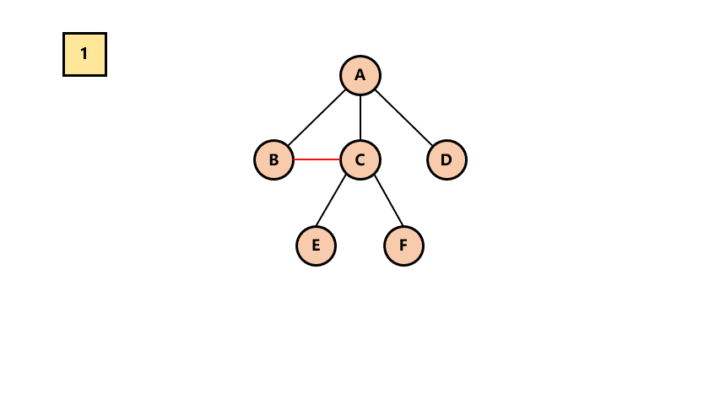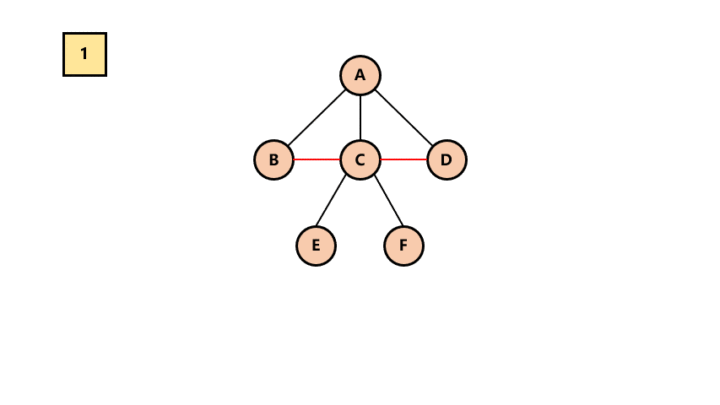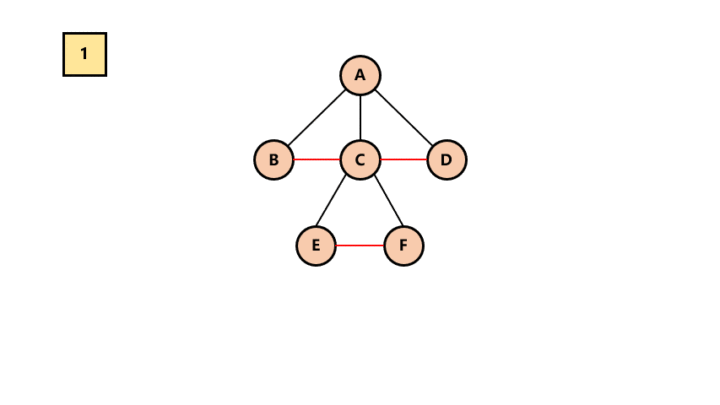
去线。树中的每个结点,只保留它与第一个孩子结点的连线, 删除其他孩子结点之间的连线。
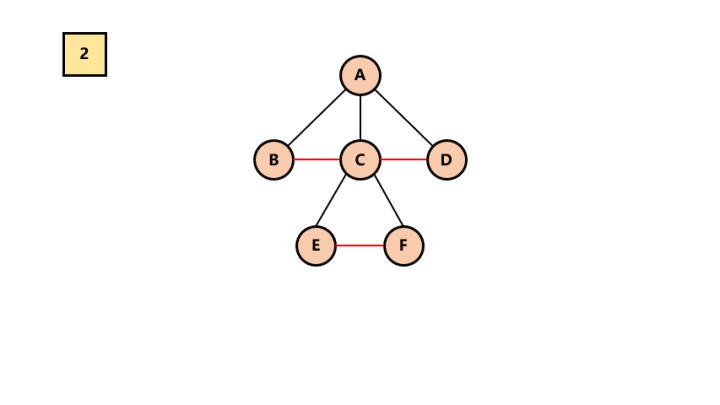
调整。以树的根结点为轴心,将整个树调节一下(第一个孩子是结点的左孩子,兄弟转过来的孩子是结点的右孩子)
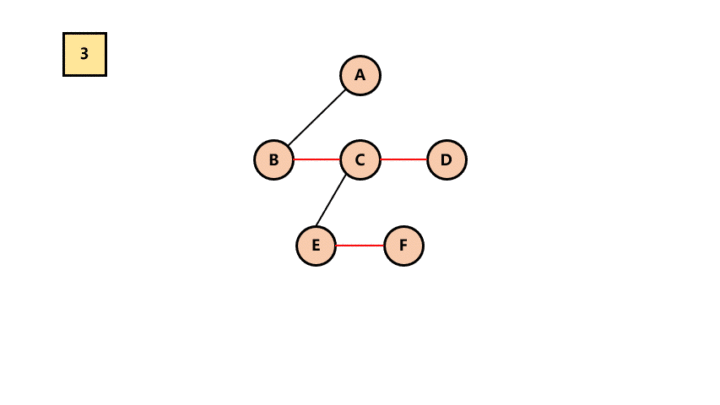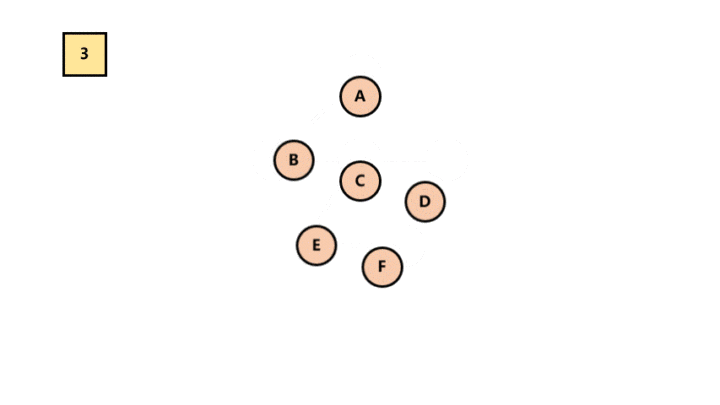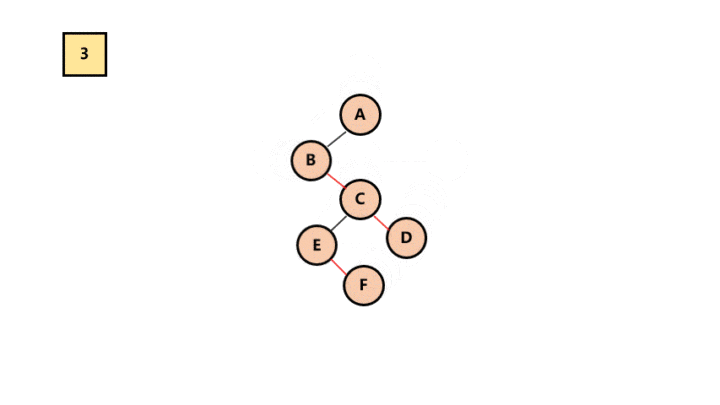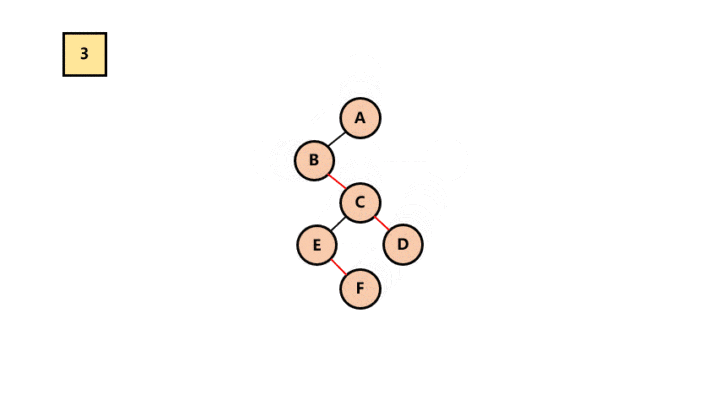
所以最终结果为:

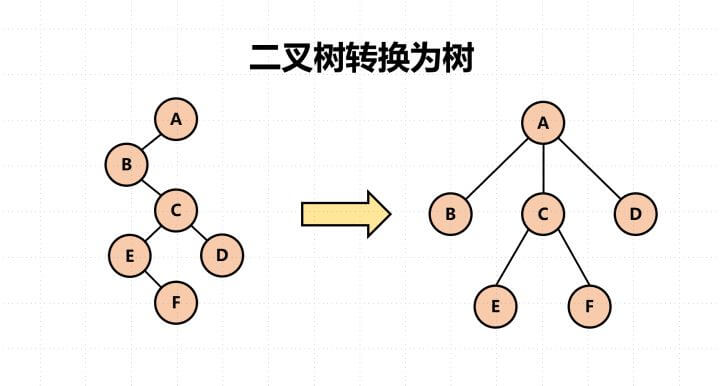
二叉树 -> 树
知道了树转换为二叉树,那么二叉树转换为树就是个逆过程呗。
调整。将二叉树从左上到右下分为若干层。然后调整成水平方向。
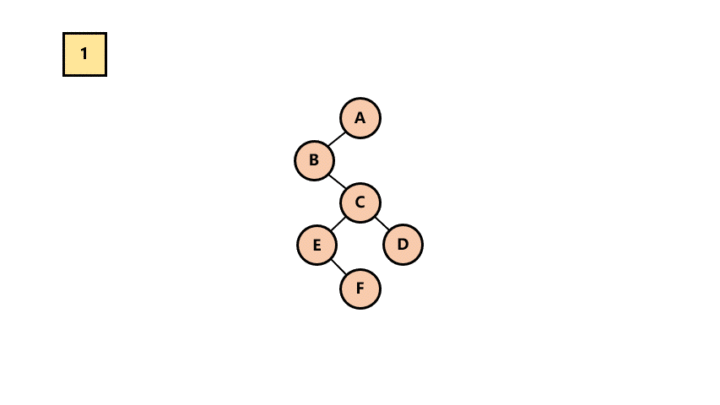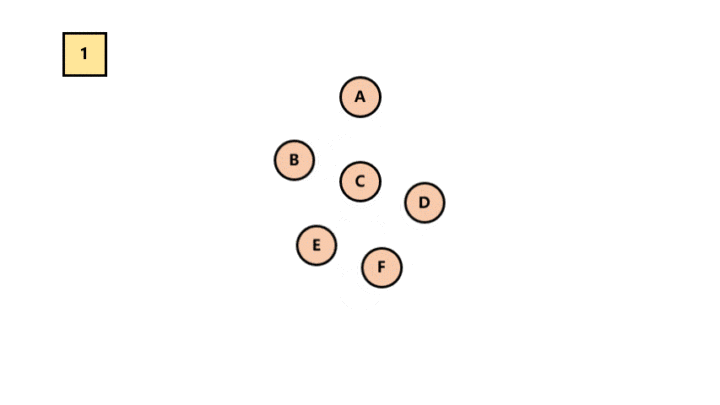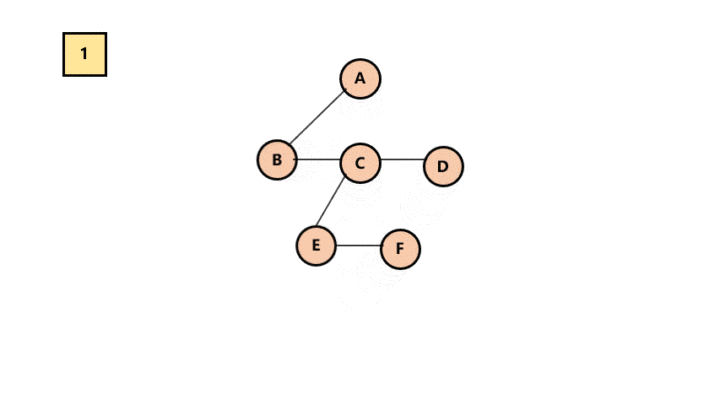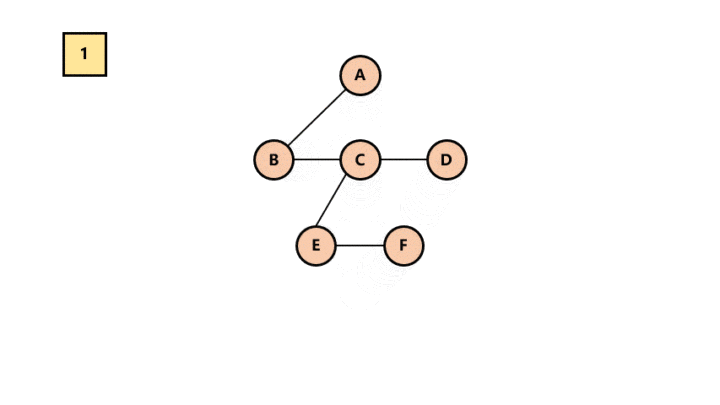
加线。找到每一层节点在其上一层的父节点,加线。

去线。去除兄弟节点之间的连线。

所以最终结果为:
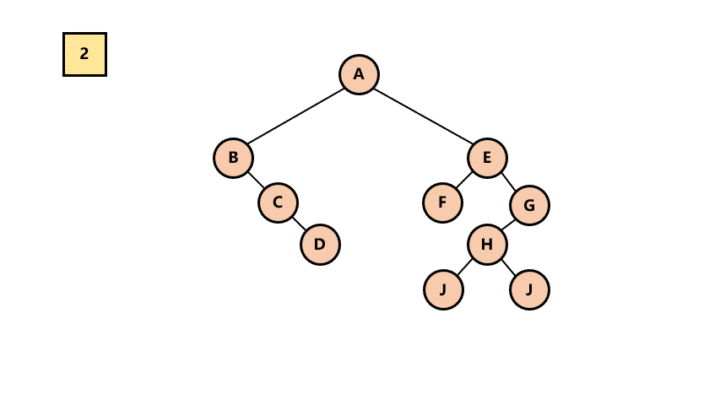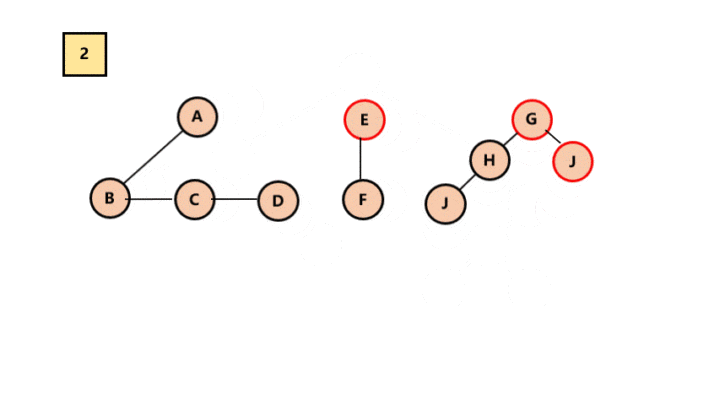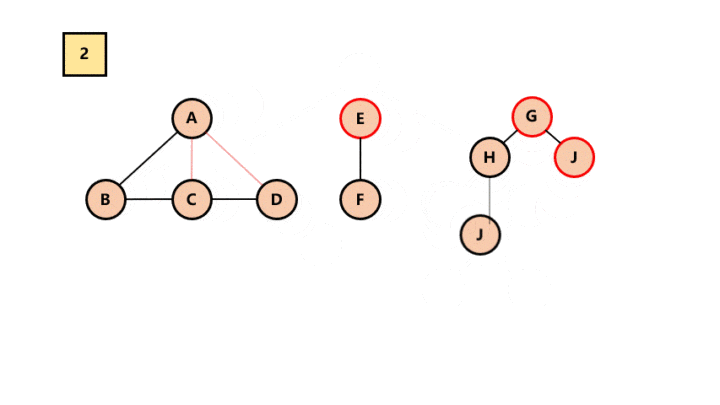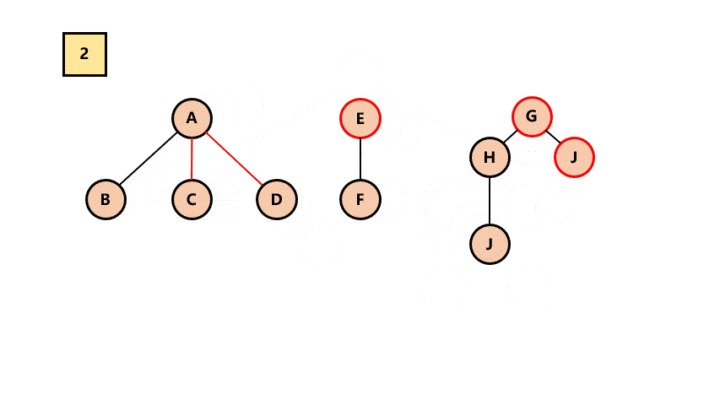
二叉树 -> 森林
在此我需要再次强调的是,根据孩子兄弟表示法,根节点是没有兄弟的。
前提:加入一棵二叉树的根节点有右孩子,则这棵二叉树能够转换为森林,否则转换为一棵树。

删除右孩子连线。
从根节点开始,若右孩子存在,则把与右孩子结点的连线删除。再查看分离后的二叉树,若其根节点的右孩子存在,则连续删除。直到所有这些根结点与右孩子的连线都删除为止。

将每棵分离后的二叉树转换为树。
所以最终结果为:
