图
弥诺陶洛斯(Minotaur)是希腊神话中半人半牛的怪物,它藏身于一个精心设计的迷宫之中。
这个迷宫的结构极其复杂,一般人一旦进入其中,都休想走出来。
不过,在公主阿里阿德涅(Ariadne)的帮助下,古希腊英雄特修斯(Theseus)还是想出了一个走出迷宫的方法。
特修斯带上一团线去闯迷宫,在入口处,他将绳线的一头绑在门上。
然后,他不断查找迷宫的各个角落,而绳线的另一头则始终抓在他的手里,跟随他穿梭于蜿蜒曲折的迷宫之中。
借助如此简单的工具,特修斯不仅终于找到了怪物并将其杀死,而且还带着公主轻松地走出了迷宫。
特修斯之所以能够成功,关键在于他借助绳线来掌握迷宫内各个通道之间的联接关系, 而在很多的问题中,掌握类似的信息都是至关重要的。 通常,这类信息所反映的都是一组对象之间的二元关系, 比如城市交通图中联接于不同点之间的街道,或 Internet 中联接于两个 IP 之间的路由等。
在某种程度上,我们前面所讨论过的树结构也可以携带和表示这种二元关系,只不过树结构中的这类关系仅限于父、子节点之间。 然而在一般情况下,我们所需要的二元关系往往是定义在任意一对对象之间。 实际上,这样的二元关系恰恰正是图论(Graph theory )
图是数据结构中重要内容。相比于线性表与树,图的结构更为复杂。 在线性表的存储结构中,数据直接按照前驱后继的线性组织形式排列。 在树的结构中,数据节点以层的方式排列,节点与节点之间是一种层次关系。 但是,在图的结构中数据之间可以有任意关系,这就使得图的数据结构相对复杂。
定义
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中, G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
例如:下图所示图
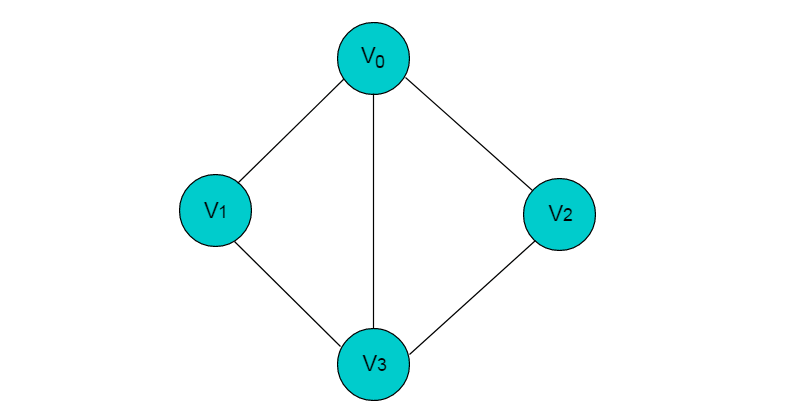
上图中,共有V0,V1,V2,V3 4个顶点,4个顶点之间共有5条边。
当线性表没有数据节点时,线性表为空表。
树中没有节点时,树为空树。
但是,在图中不允许没有顶点,但是可以没有边。
图(Graph)可以表示为 G = (V, E)
- 其中集合 V 中的对象称作顶点(Vertex)
- 而集合 E 中的每一元素都对应于 V 中某一对顶点⎯⎯说明这两个顶点之间存在某种关系⎯⎯称作边(Edge)
这里还约定 V 和 E 都是有限集,通常记 n = |V|、m = |E|。
对于图的定义,我们需要明确几个注意的地方:
- 线性表中我们把数据元素叫元素,树中叫结点,在图中数据元素我们则称之为顶点(Vertex)。
- 线性表可以没有数据元素,称为空表,树中可以没有结点,叫做空树,而图结构在咱国内大部分的教材中强调顶点集合V要有穷非空。
- 线性表中,相邻的数据元素之间具有线性关系,树结构中,相邻两层的结点具有层次关系,而图结构中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
无向边
若顶点 x 和 y 之间的边没有方向,则称该边为无向边(x,y),(x,y) 与 (y,x) 意义相同,表示x和y之间有连接。
下图所示图中的边均为无向边。
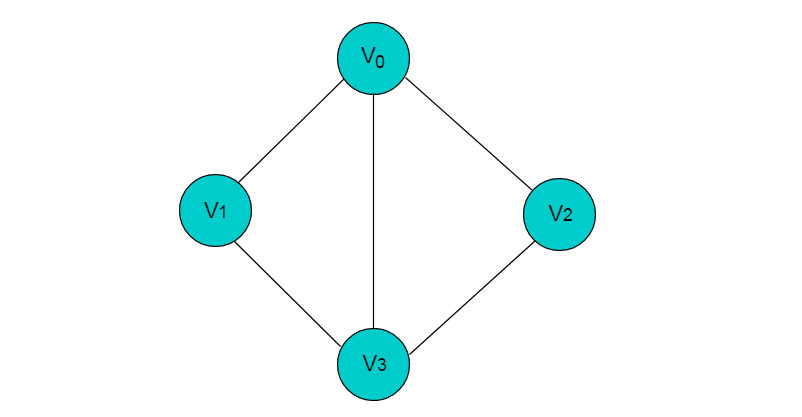
有向边
有向边:若顶点 x 和 y 之间的边有方向,则称该边为有向边
下图所示图中的边为有向边。
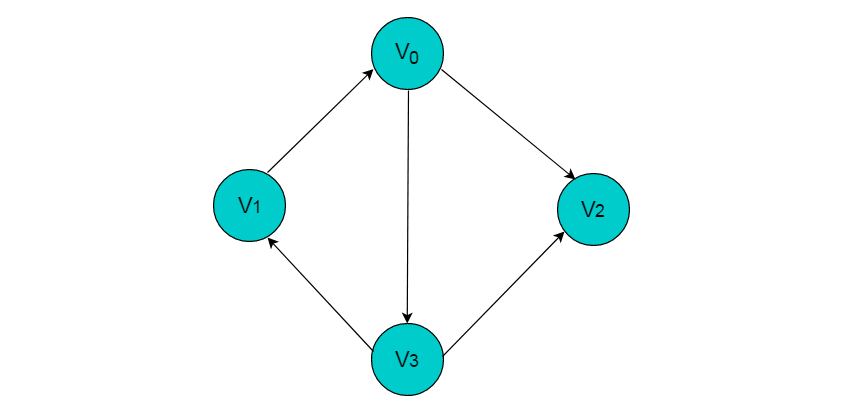
无向图
若图中任意两个顶点之间的边均是无向边,则称该图为无向图。
有向图
若图中任意两个顶点之间的边均是有向边,则称该图为有向图。
混合图
顶点与顶点的度
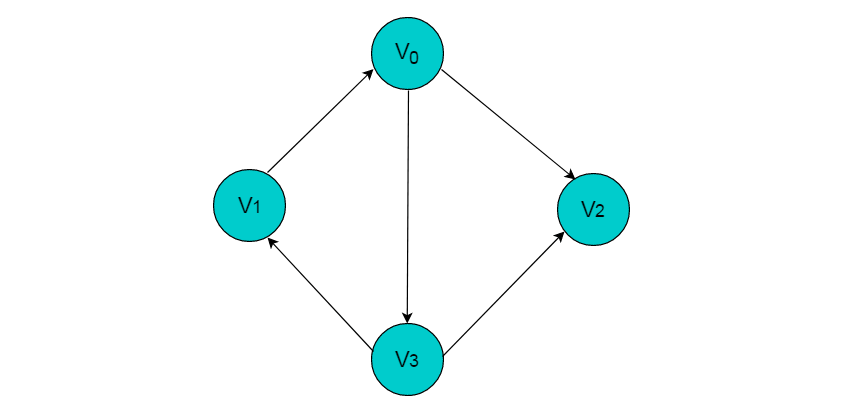
- 顶点的度:顶点V的度是和V相关联的边的数目,记为TD(V)。 上图中,V0顶点的度为3。
- 入度:以顶点v为头的边的数目,记为ID(V)。 上图中,V0的入度为1。
- 出度:以顶点v为尾的边的数目,记为OD(V)。 上图中,V0的出度为2。
- 顶点的度 = 入度 + 出度。 即TD(V) = ID(V) + OD(V)。
邻接
邻接是两个顶点之间的一种关系。如果图包含(u,v),则称顶点 v 与顶点 u 邻接。 在无向图中,这也暗示了顶点 u 也与顶点 v 邻接。换句话说,在无向图中邻接关系是对称的。
路径
在图中,依次遍历顶点序列之间的边所形成的轨迹。
例如:在下图中依次访问顶点 V0 、V3 和 V2 ,则构成一条路径。
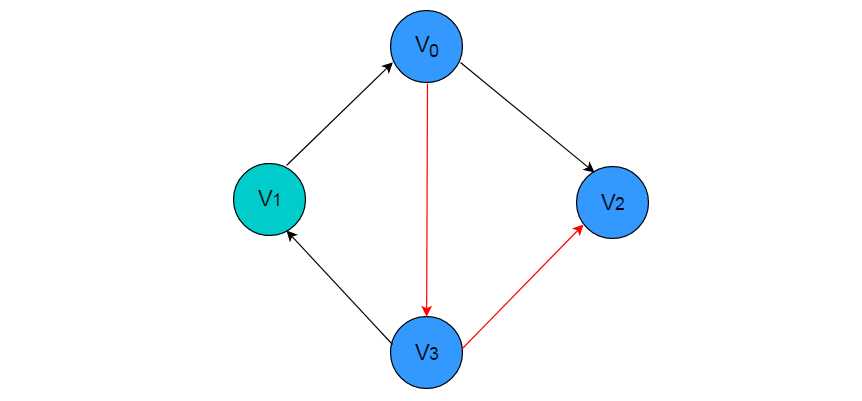
完全图
每个顶点都与其他顶点相邻接的图。
无向完全图
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。 (含有n个顶点的无向完全图有(n×(n-1))/2条边)
下图为无向完全图
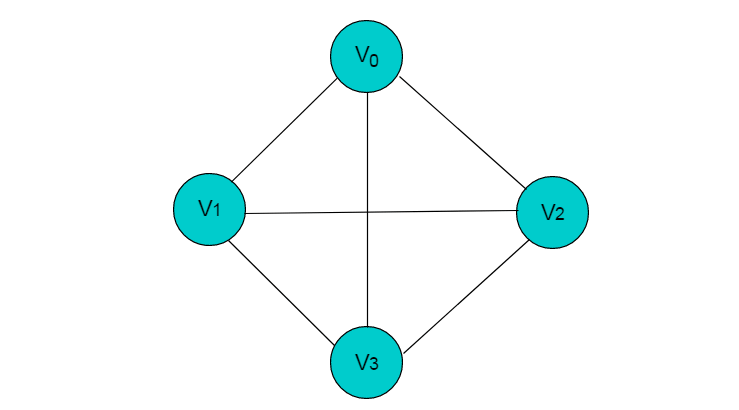
有向完全图
在有向图中,如果任意两个顶点之间都存在方向互为相反的两条边,则称该图为有向完全图。 (含有 n 个顶点的有向完全图有 n×(n-1) 条边)
下图为有向完全图。
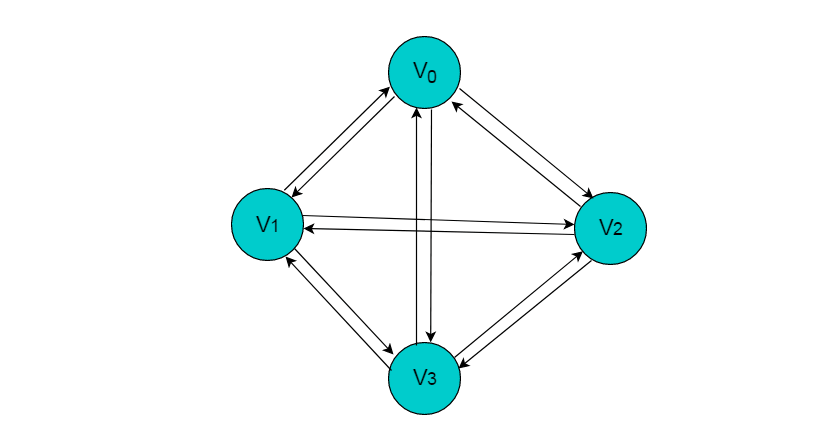
通路、环路及可达分量
通路——所谓图中的一条通路或路径(Path),就是由(不一定互异的)m+1 个顶点与 m 条边交替构成的一个序列ρ = {v 0 , e 1 , v 1 , e 2 , v 2 , …, e m , v m },m ≥ 0,而且 e i = (v i-1 , v i ),1 ≤ i ≤ m。
环路—— 长度 m ≥ 1 的路径,若第一个顶点与最后一个顶点相同,则称之为环路(Cycle)。
可达分量——对于指定的顶点 s,从 s 可达的所有顶点所组成的集合,称作 s 在 G 中对应的可达分量,记作 V r (G, s)。
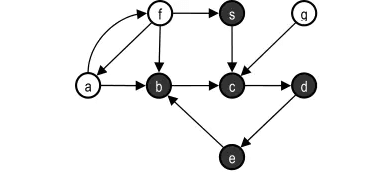
连通图
在无向图 G 中,如果从顶点 v 到顶点 v' 有路径,则称 v 和 v' 是连通的。 如果对于图中任意两个顶点 vi 、vj ∈E, vi,和vj都是连通的,则称 G 是连通图,否则图为非连通图。
例如:图4.1所示图,图中顶点A、B、C、D是连通的,但是其中任一顶点与顶点E或者顶点F之间没有路径, 因此图4.1中所示的图为非连通图。
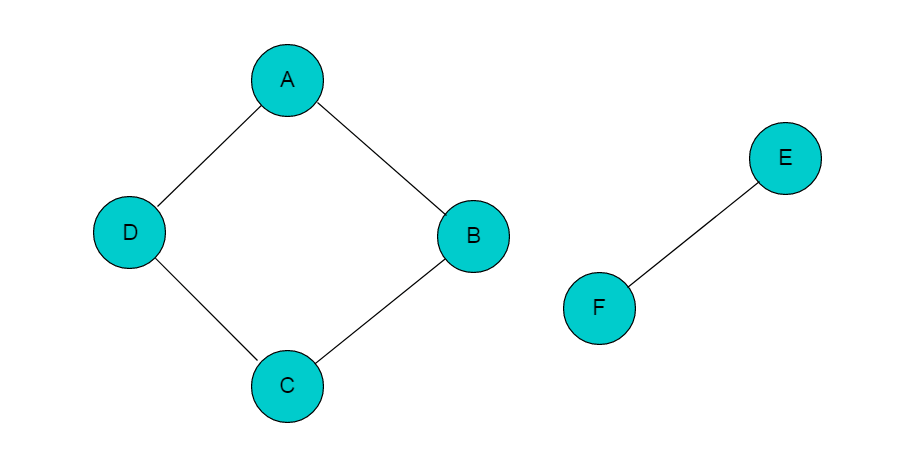
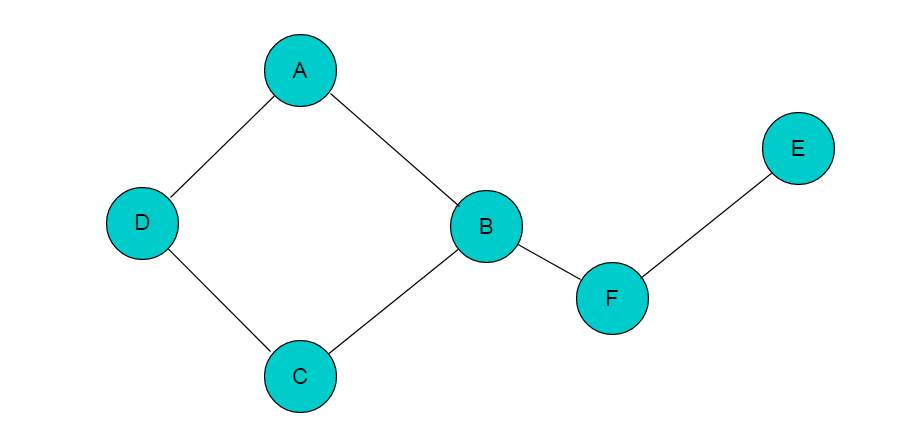
若添加顶点B与顶点F之间的邻接边,则图变为连通图,如下图所示:
树、森林和连通图
无向图 G = (V, E):
若 G 中不含任何环路,则称之为森林(Forest)。
连通的森林称作树(Tree)。
不难看出,森林中的每一连通分量都是一棵树,反之亦然。
设 G 为由 n 个顶点与 m 条边组成一幅无向图:
- 若 G 是连通的,则 m ≥ n-1;

- 若 G 是一棵树,则 m = n-1;

- 若 G 是森林,则 m ≤ n-1。

面试中关于图的常见问题
- 实现广度和深度优先搜索
- 检查图是否为树
- 计算图的边数
- 找到两个顶点之间的最短路径