B+ 树

B+树是对B树的一种变形树,它与B树的差异在于:
- 有k个子结点的结点必然有k个关键码;
- 非叶结点仅具有索引作用,跟记录有关的信息均存放在叶结点中。
- 树的所有叶结点构成一个有序链表,可以按照关键码排序的次序遍历全部记录。
如下图,是一个B+树:
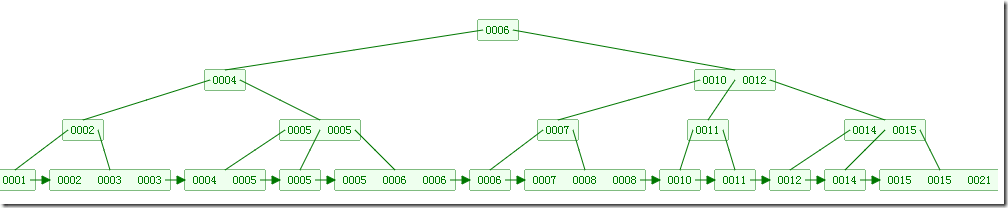
下图是B+树的插入动画:

B和B+树的区别
B+树的非叶子结点只包含导航信息,不包含实际的值,所有的叶子结点和相连的节点使用链表相连, 便于区间查找和遍历。
B+树的优点:
由于B+树在内部节点上不包含数据信息,因此在内存页中能够存放更多的key。 数据存放的更加紧密, 具有更好的空间局部性。因此访问叶子节点上关联的数据也具有更好的缓存命中率。 B+树的叶子结点都是相链的,因此对整棵树的便利只需要一次线性遍历叶子结点即可。 而且由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。 相邻的元素可能在内存中不相邻,所以缓存命中性没有B+树好。
B树得优点
由于B树的每一个节点都包含key和value,因此经常访问的元素可能离根节点更近,因此访问也更迅速。
下面是B 树和B+树的区别图:
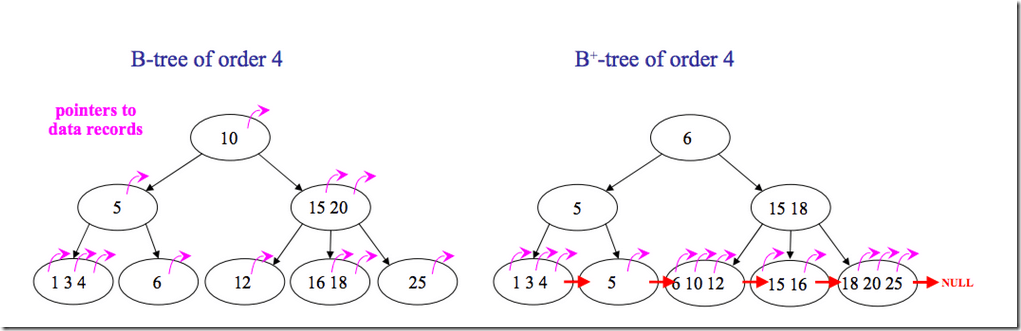
下面我们看一个B+树的例子,感受感受它吧!
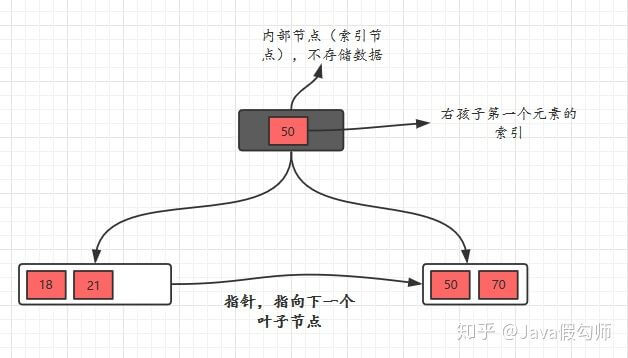
插入操作
对于插入操作很简单,只需要记住一个技巧即可: 当节点元素数量大于m-1的时候,按中间元素分裂成左右两部分,中间元素分裂到父节点当做索引存储, 但是,本身中间元素还是分裂右边这一部分的。
下面以一颗5阶B+树的插入过程为例,5阶B+树的节点最少2个元素,最多4个元素。
插入5,10,15,20
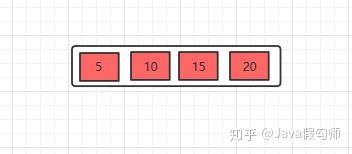
插入25,此时元素数量大于4个了,分裂
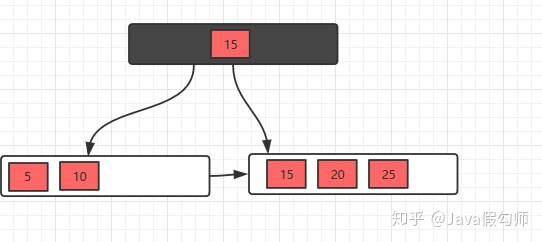
接着插入26,30,继续分裂
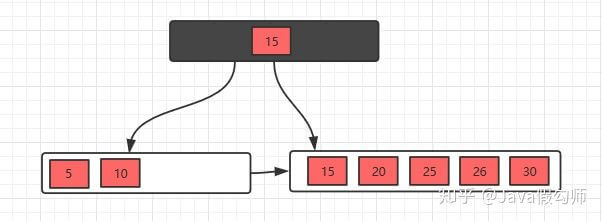
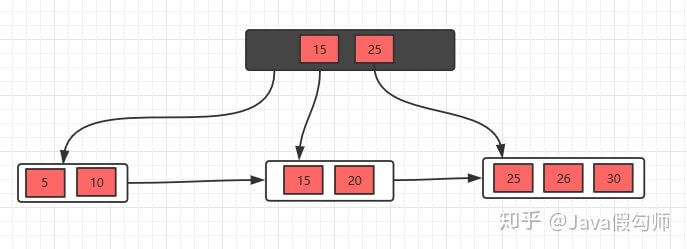
有了这几个例子,相信插入操作没什么问题了,下面接着看看删除操作。
删除操作
对于删除操作是比B树简单一些的,因为叶子节点有指针的存在,向兄弟节点借元素时,不需要通过父节点了, 而是可以直接通过兄弟节移动即可(前提是兄弟节点的元素大于m/2), 然后更新父节点的索引;如果兄弟节点的元素不大于m/2(兄弟节点也没有多余的元素), 则将当前节点和兄弟节点合并,并且删除父节点中的key, 下面我们看看具体的实例。
初始状态
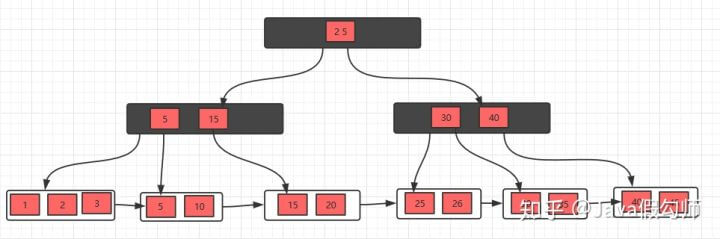
删除10,删除后,不满足要求,发现左边兄弟节点有多余的元素,所以去借元素,最后,修改父节点索引
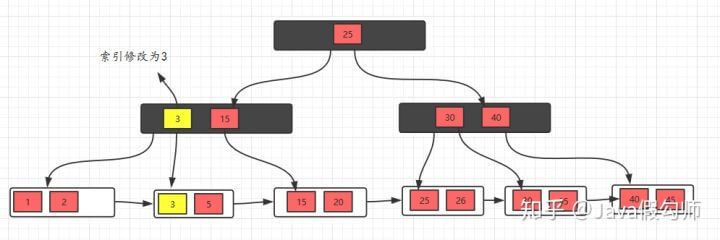
删除元素5,发现不满足要求,并且发现左右兄弟节点都没有多余的元素, 所以,可以选择和兄弟节点合并,最后修改父节点索引
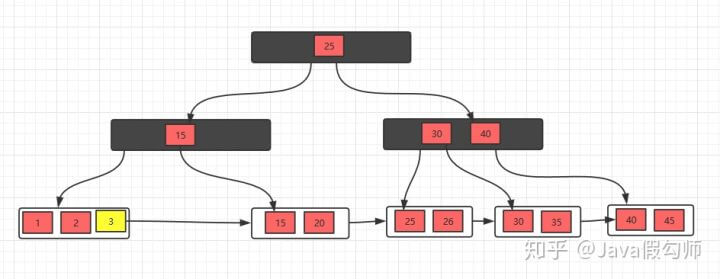
发现父节点索引也不满足条件,所以,需要做跟上面一步一样的操作
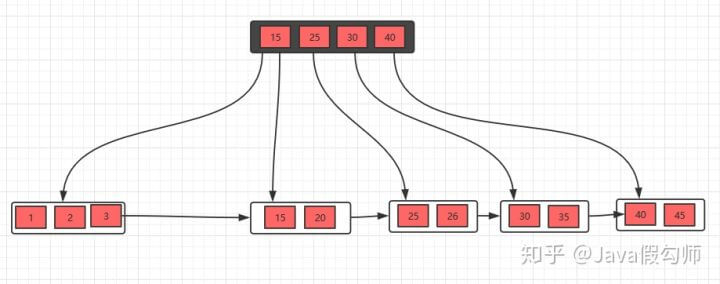
这样,B+树的删除操作也就完成了,是不是看完之后,觉得非常简单!
为什么说B+树比B树更适合做操作系统的数据库索引和文件索引?
- B+树的磁盘读写的代价更低
B+树内部结点没有指向关键字具体信息的指针,这样内部结点相对B树更小。
- B+树的查询更加的稳定
因为非终端结点并不是最终指向文件内容的结点,仅仅是作为叶子结点中关键字的索引。这样所有的关键字的查找都会走一条从根结点到叶子结点的路径。所有的关键字查询长度都是相同的,查询效率相当。