选择排序
选择排序 是表现最稳定的排序算法之一 , 因为无论什么数据进去都是O(n2)的时间复杂度 , 所以用到它的时候,数据规模越小越好。 唯一的好处可能就是不占用额外的内存空间了吧。 理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧。
选择排序(Selection-sort) 是一种简单直观的排序算法。 它的工作原理:首先在未排序序列中找到最小(大)元素, 存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小 (大)元素,然后放到已排序序列的末尾。 以此类推,直到所有元素均排序完毕。
算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。 具体算法描述如下:
- 步骤1:初始状态:无序区为R[1…n],有序区为空;
- 步骤2:第i趟排序(i=1,2,3…n-1)开始时, 当前有序区和无序区分别为R[1…i-1]和R(i…n)。 该趟排序从当前无序区中-选出关键字最小的记录 R[k], 将它与无序区的第1个记录R交换, 使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- 步骤3:n-1趟结束,数组有序化了。
动图演示
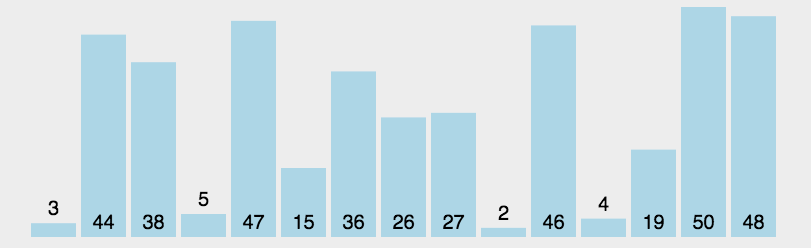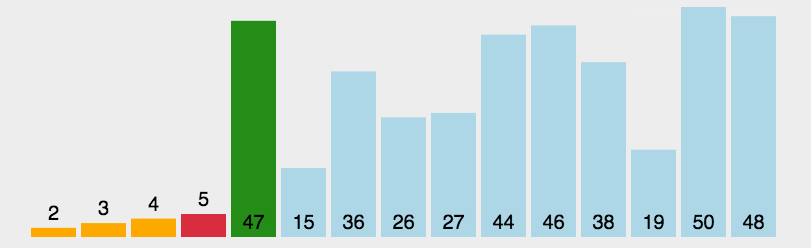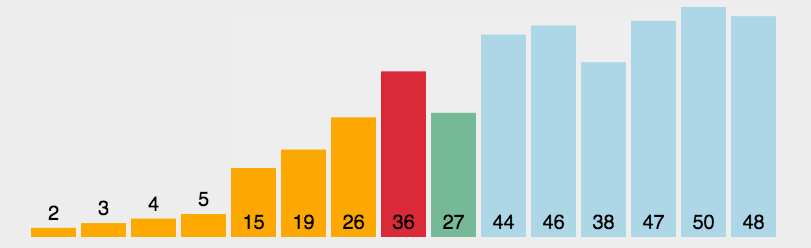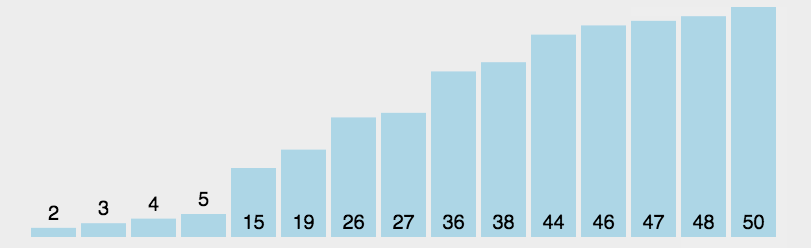
代码实现
package algorithm.sort;
import java.util.Arrays;
public class Selection {
public static void main(String[] args) {
int[] array = {1, 2, 9, 4, 6, 7, 8, 3, 0, 5};
System.out.println("原始数组:" + Arrays.toString(array));
System.out.println("排序后数组:" + Arrays.toString(Selection.selection(array)));
}
private static int[] selection(int[] array) {
if(array.length == 0){
return array;
}
int arrayLength = array.length;
int item = 0;
int minIndex = 0;
for (int i = 0; i < arrayLength; i++) {
minIndex = i;
for (int j = i; j < arrayLength; j++) {
if (array[j] < array[minIndex]){
minIndex = j;
}
}
if (minIndex != i){
item = array[i];
array[i] = array[minIndex];
array[minIndex] = item;
}
}
return array;
}
} ```
算法分析
表现最稳定的排序算法之一,因为无论什么数据进去都是O(n2)的时间复杂度, 所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。 理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧。
- 最佳情况:T(n) = O(n2)
- 最差情况:T(n) = O(n2)
- 平均情况:T(n) = O(n2)
选择排序的交换操作介于 0 和 (n - 1) 次之间。 选择排序的比较操作为 n (n - 1) / 2 次之间。 选择排序的赋值操作介于 0 和 3 (n - 1) 次之间。
比较次数O(n^2),比较次数与关键字的初始状态无关 ,总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2。 交换次数O(n),最好情况是,已经有序,交换0次; 最坏情况交换n-1次,逆序交换n/2次。交换次数比冒泡排序少多了 ,由于交换所需CPU时间比比较所需的CPU时间多, n值较小时,选择排序比冒泡排序快。
稳定性
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的, 在剩余元素里面给第二个元素选择第二小的,依次类推, 直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。 那么,在一趟选择,如果一个元素比当前元素小, 而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。 比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换, 那么原序列中两个5的相对前后顺序就被破坏了, 所以选择排序是一个不稳定的排序算法